openwebui-v0.6.5学习02-常用配置与使用

一、管理员面板

以“管理员”权限组的用户比如超级管理员登录系统，才能看到与操作“管理员面板”。

image-20250612113108218

1.1 用户

1.1.1 概述中的用户管理

安装open-webui的最后步骤，自行注册的用户是超级管理员，无法被删除。可以修改其用户名与密码，邮箱无法修改。

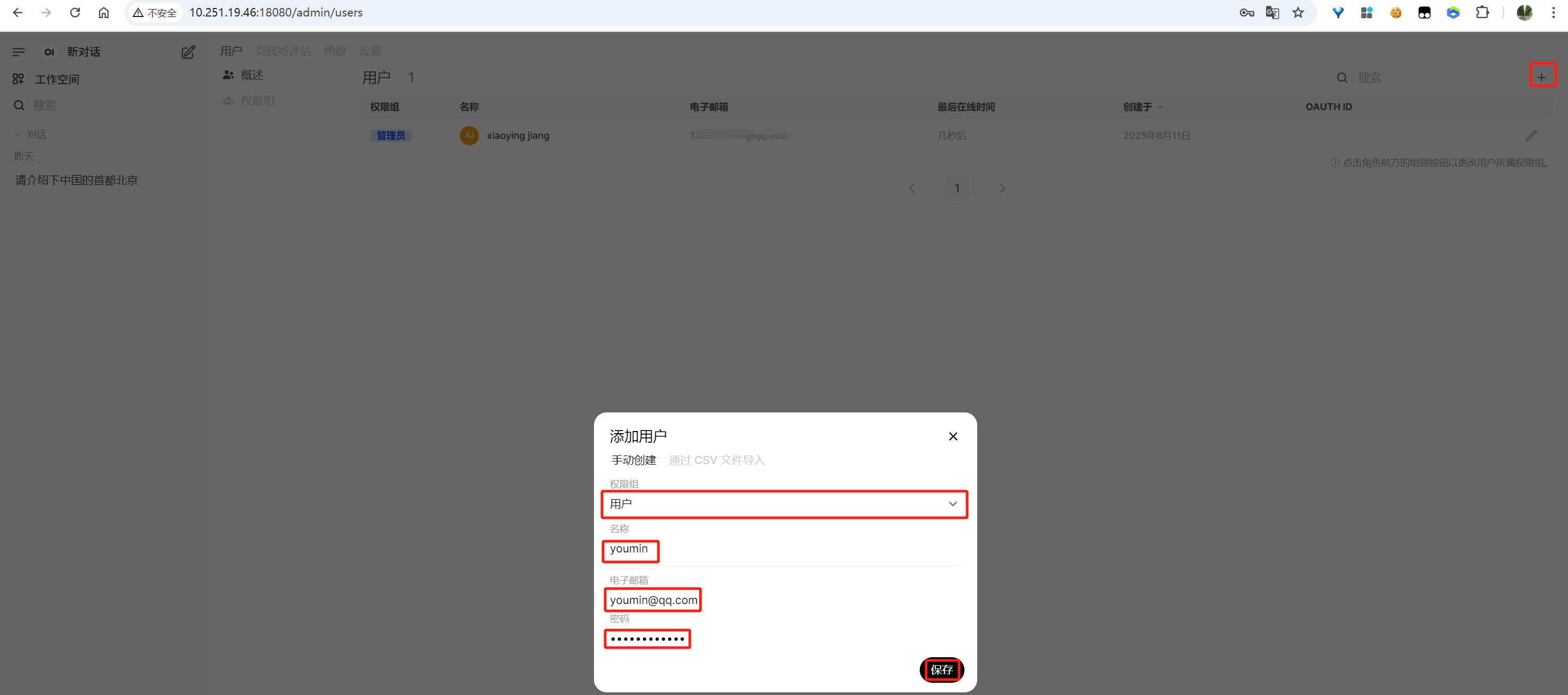
  • 添加用户
    • 添加用户时，需要选择其权限组，有“待激活、用户、管理员”三个选项可选。拥有“待激活”权限的用户，登录后无法进行实际操作，需要联系管理员进行激活；拥有“用户”权限的用户，是普通用户，拥有较小的操作权限比如可以选择LLM进行对话，可以管理自己的信息，但无法修改系统配置信息与管理其他用户等；拥有“管理员”权限的用户，在前者的基础上，进行拥有修改系统配置信息与管理其他用户等的权限，此类型用户无法被删除，如果要删除先要将其修改为拥有“用户”权限的用户。
    • 添加用户时填写的邮箱不会进行真正的校验，如果是开发或自用，随便填写个邮箱账号即可。
image-20250612122503748

  • 编辑用户与删除用户

    此处用户可以被删除、编辑。此处用户的权限组只能是系统默认创建的“待激活、用户、管理员”的3个权限组中的一个。

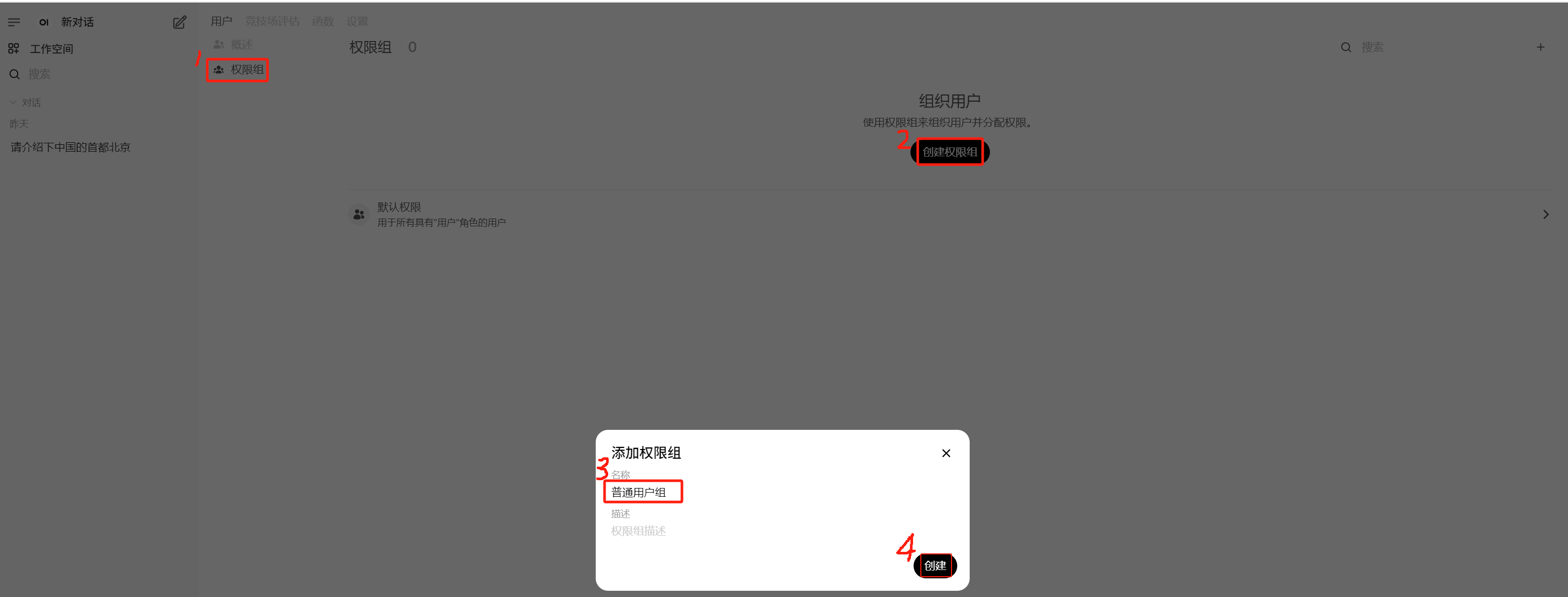
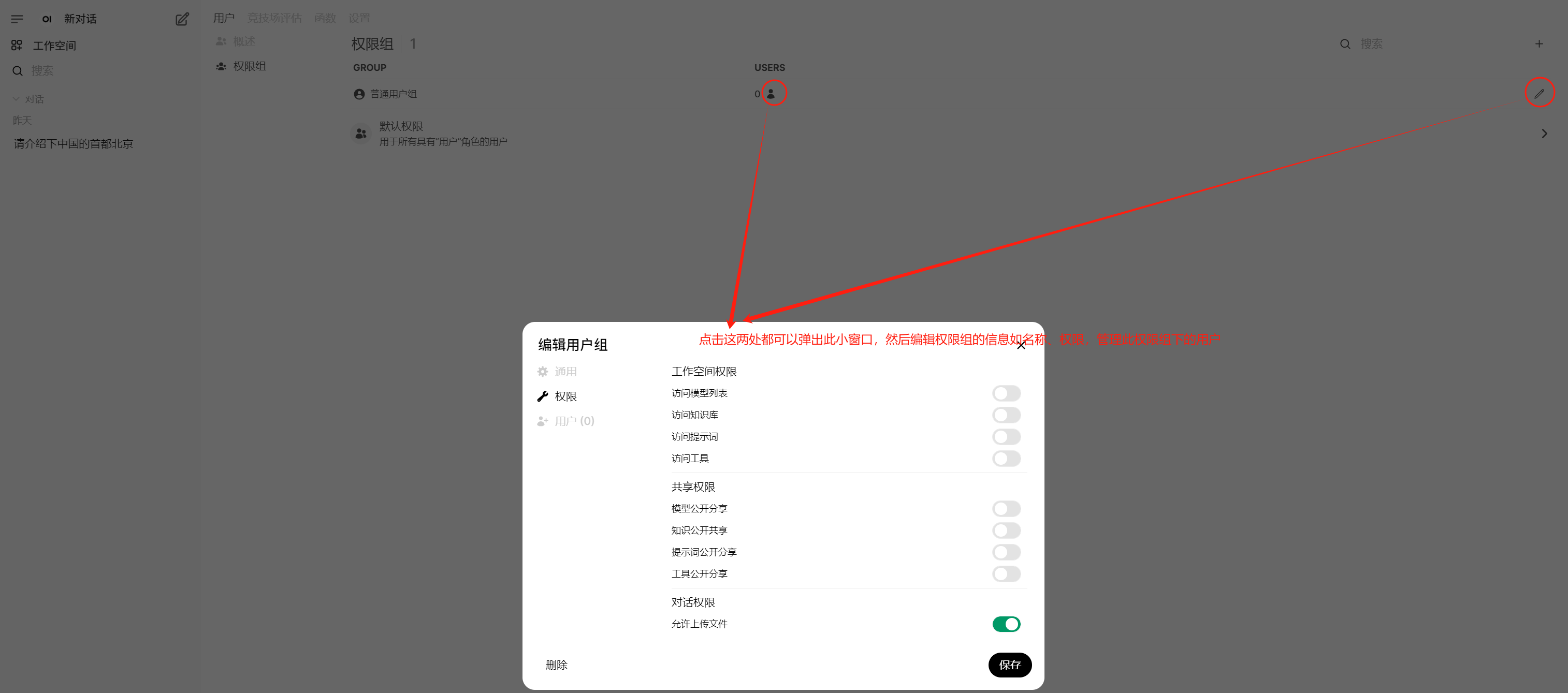
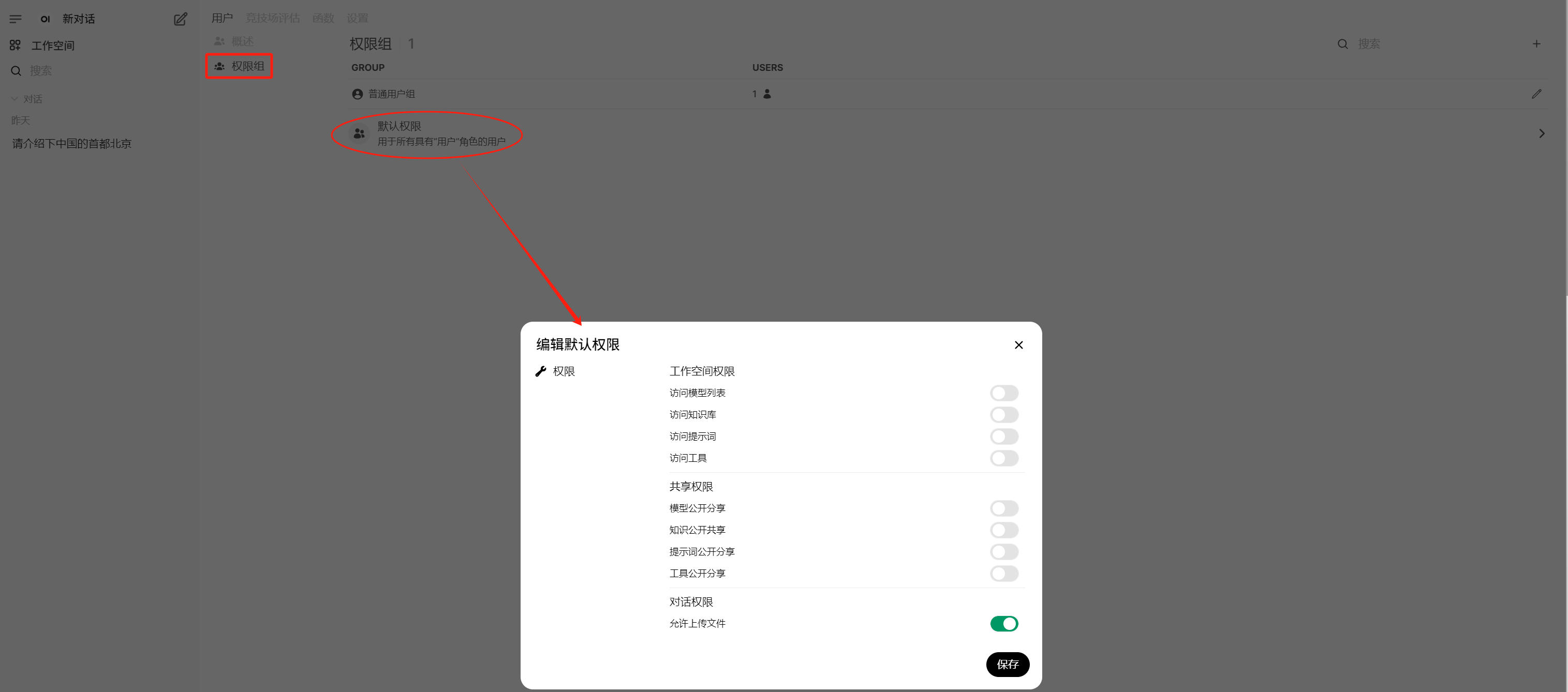
1.1.2 权限组管理

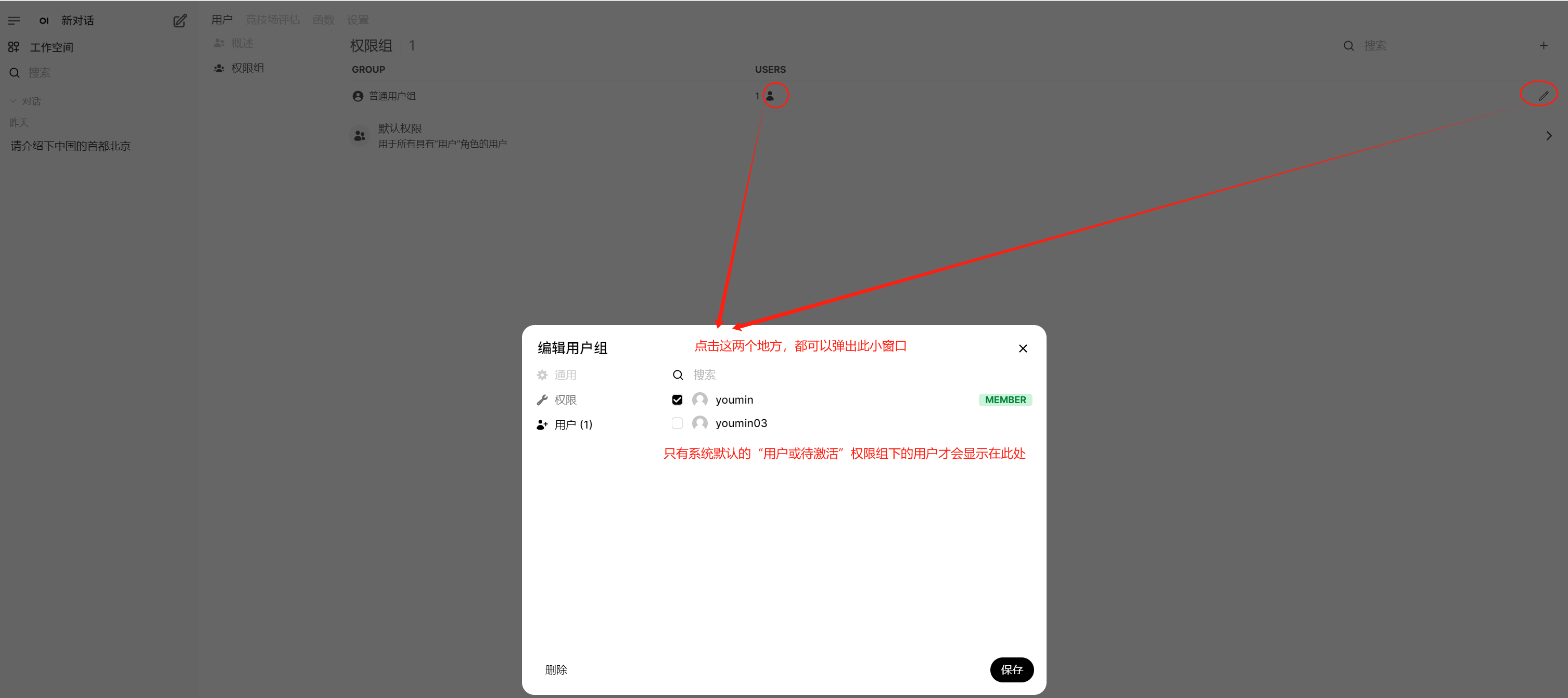
此处为自定义权限组，跟系统默认存在的3个权限组（管理员、用户、待激活）是不同但又有联系的概念。自定义权限组可以添加系统中的用户，但只有系统默认的“用户或待激活”权限组下的用户才能添加进来。

  • 创建权限组：
image-20250612143227393
  • 编辑权限组：
image-20250612143554275
  • 为权限组添加、删除用户：
image-20250612150521690
  • 默认权限：

​ 系统默认的“用户”权限组的权限可以进行编辑。但如果此处权限与自定义权限组的权限不同或冲突时，谁的权限较大以谁为准（个人觉得应该以自定义权限组的权限为准）。

image-20250612145359065

1.2 设置

如果在页面做了修改，一定点击页面右下角的“保存”按钮保存所做修改，否则无效。

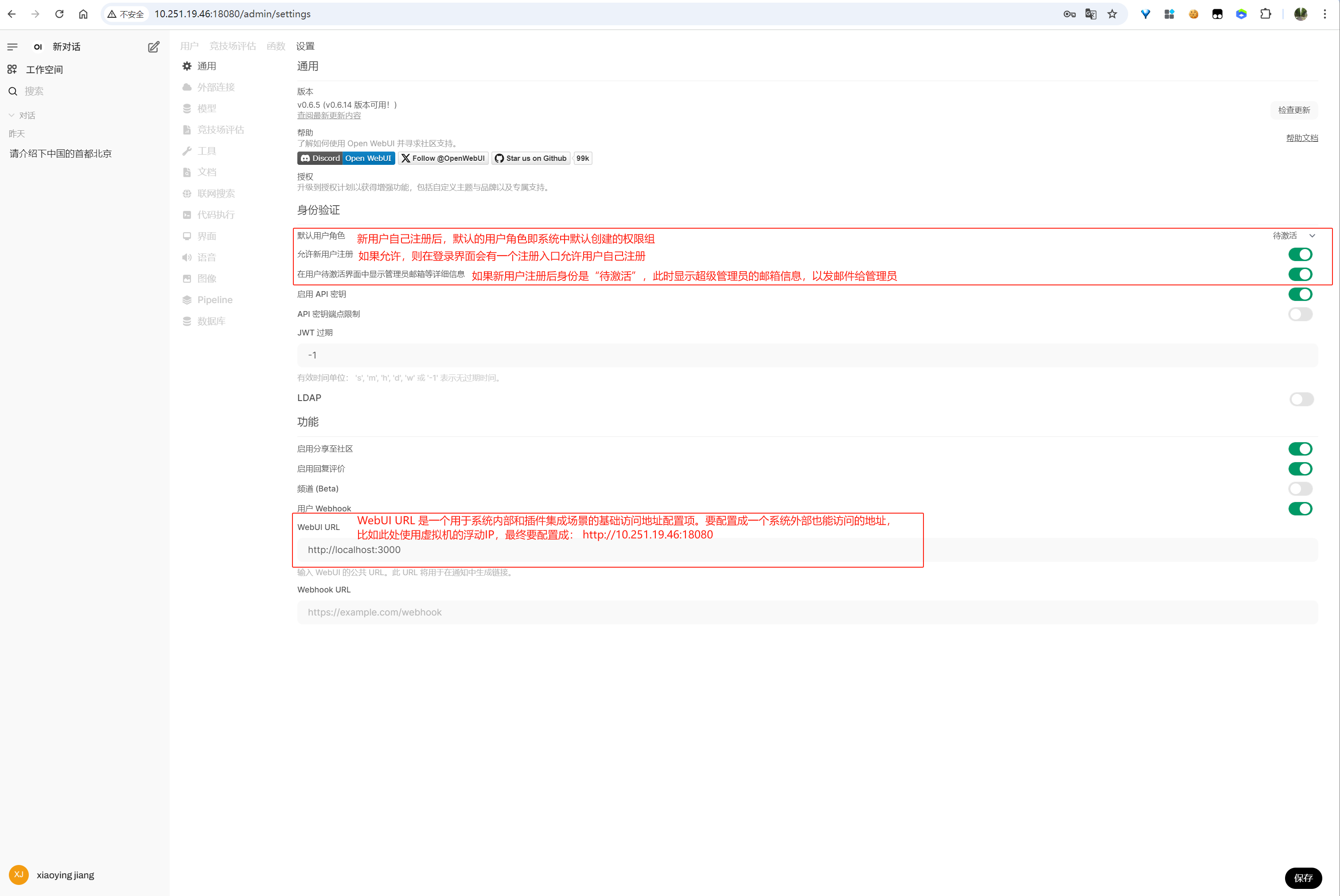
1.2.1 通用

image-20250612155144746

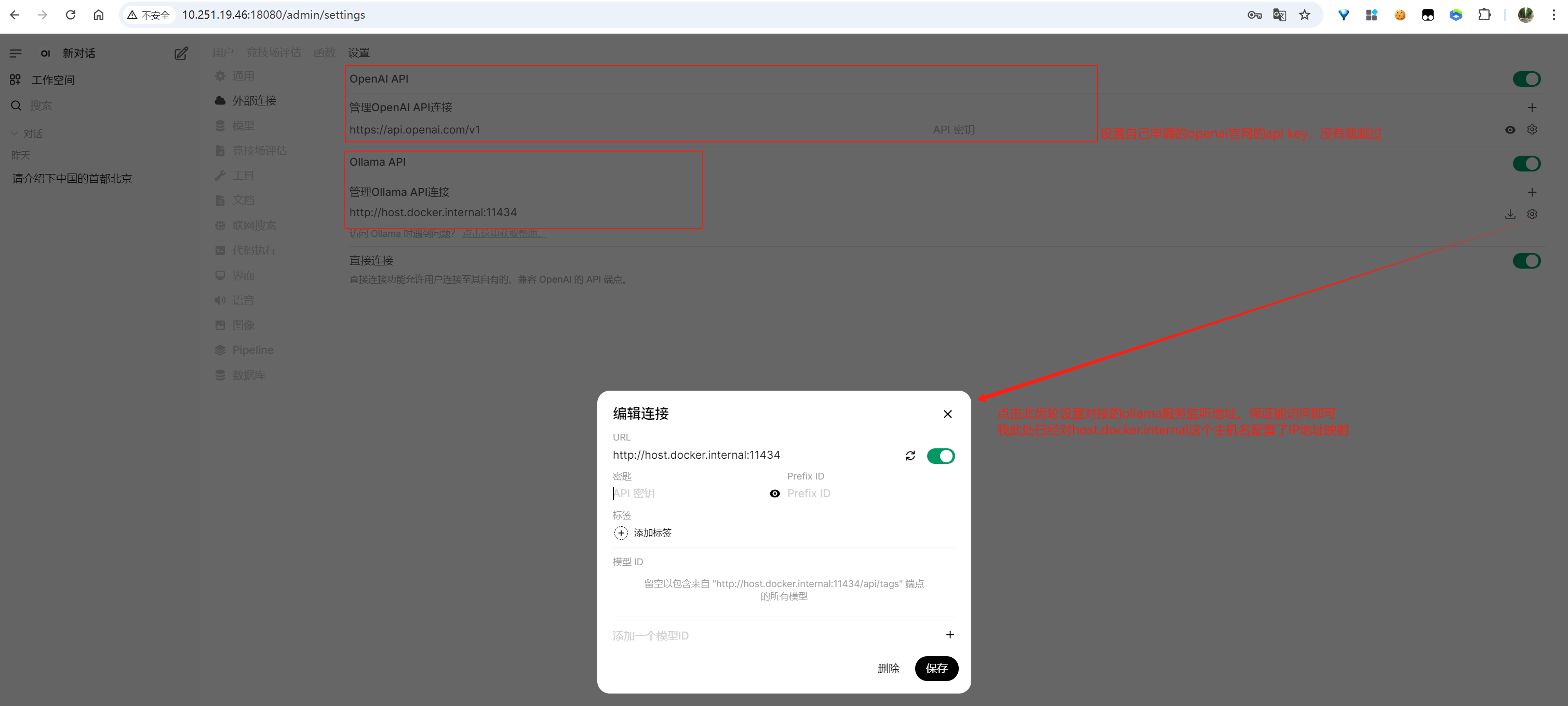
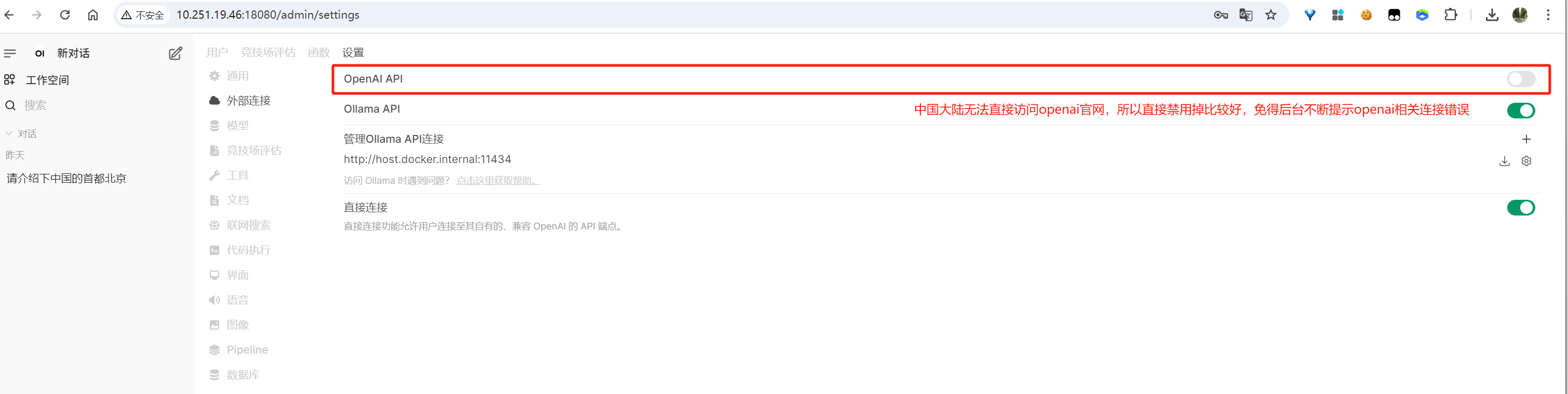
1.2.2 外部连接

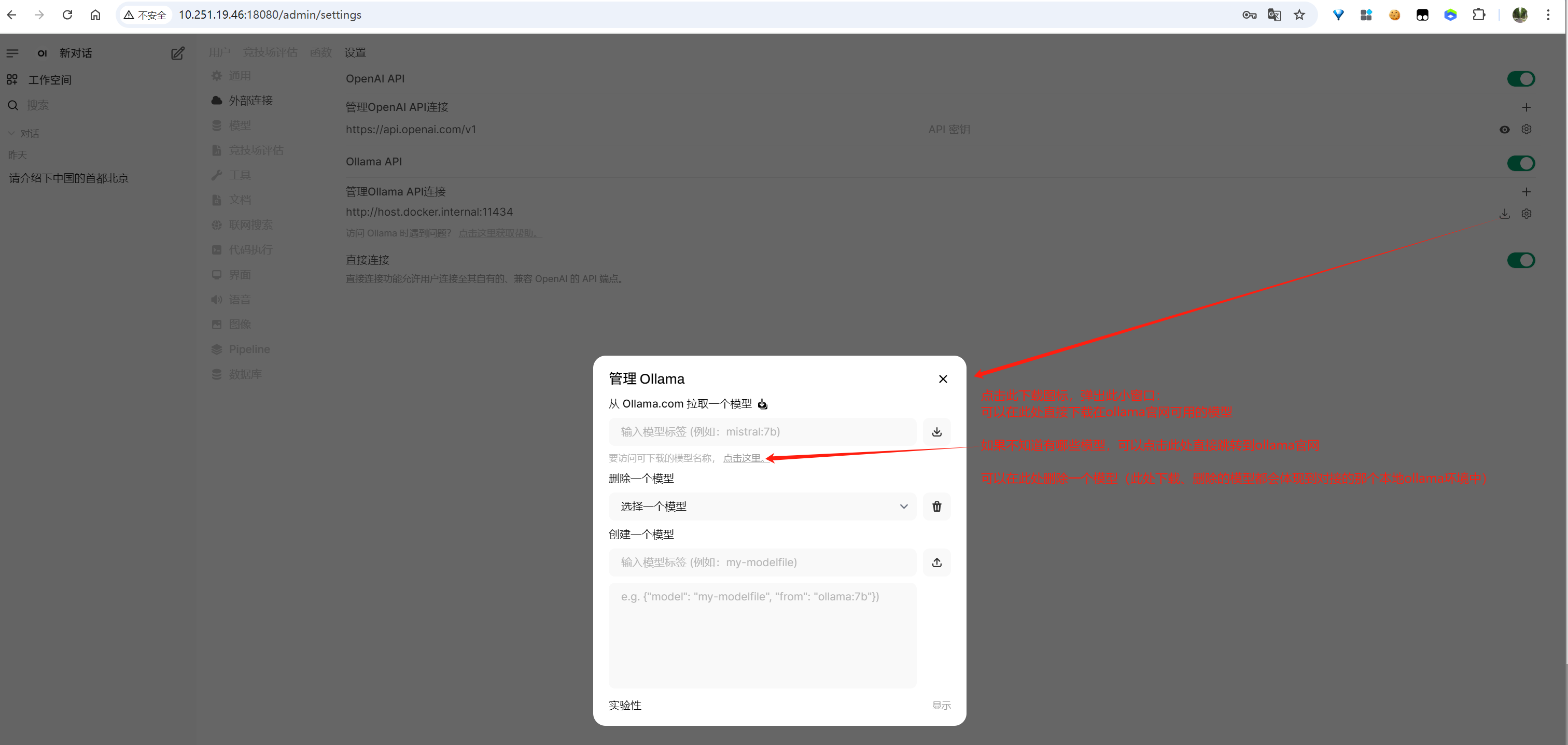
image-20250612155734260
image-20250612170001569
image-20250612160252442

创建一个模型时，可以上述小窗口的json输入框中输入如下内容（qwen2.5:3b在本地ollama环境中是否存在都没关系，如果不存在的话，ollama就自动尝试去下载），然后点击右上角的上传图标，就会从qwen2.5:3b复制出一个模型my-modelfile:latest

1
{"model":"my-modelfile", "from":"qwen2.5:3b"}

1.2.3 模型

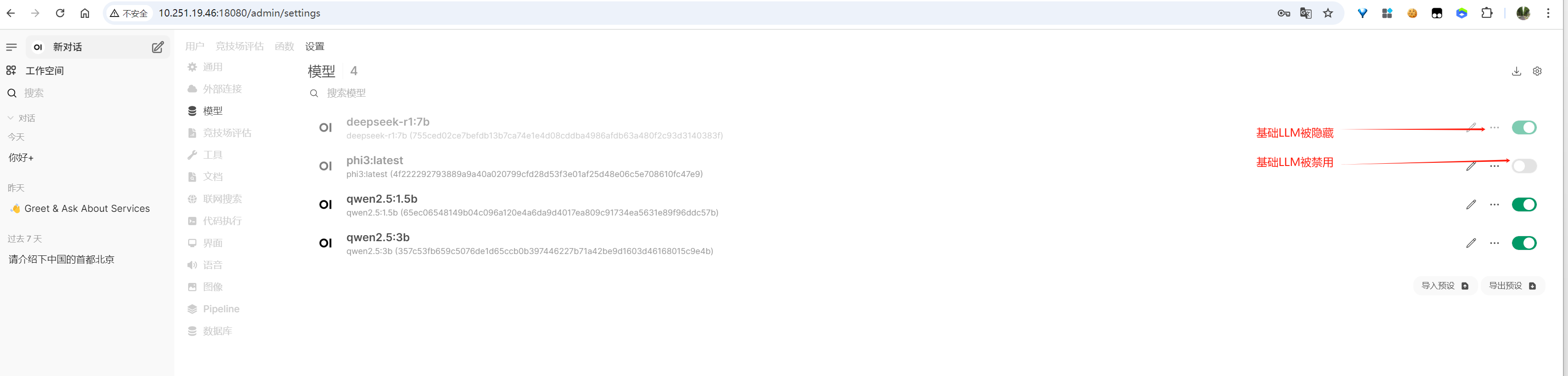
image-20250613103947977

  • 相关说明：

    • （1）LLM被禁用后，就无法被看见与使用

    • （2）LLM被隐藏后，只是无法被看见，有权限的用户如果知道某个LLM仍可直接使用

    • （3）此页面看到的LLM都是基础模型，可以修改基础模型的的信息如名称、可见性、系统提示词、知识库、工具等

    • ​ 如果基础模型的可见性是私有并分配给某个（些）自定义权限组了，则其他自定义权限组中用户则无法看见与使用此基础模型（只有系统默认“用户、待激活”角色的用户才能添加到自定义权限组），系统默认“管理员”角色中的用户仍可继续看见与使用此基础模型。

    • （4）如果基础模型的可见性是私有并分配给某个（些）自定义权限组g1了，但在工作空间中基于基础LLM创建一个自定义LLM，如果此自定义LLM是私有的并设置为自定义权限组g1可见，则其他自定义权限组不可看到与使用。

    • ​ 如果基础模型的可见性是私有并分配给某个（些）自定义权限组g1了，但在工作空间中基于基础LLM创建一个自定义LLM，如果此自定义LLM是私有的，可以被设置为自定义权限组g2可见，其他自定义权限组不可看到与使用。

    • ​ 就是说自定义权限组中的用户只能看到“工作空间”中分配给自己权限组的自定义LLM。

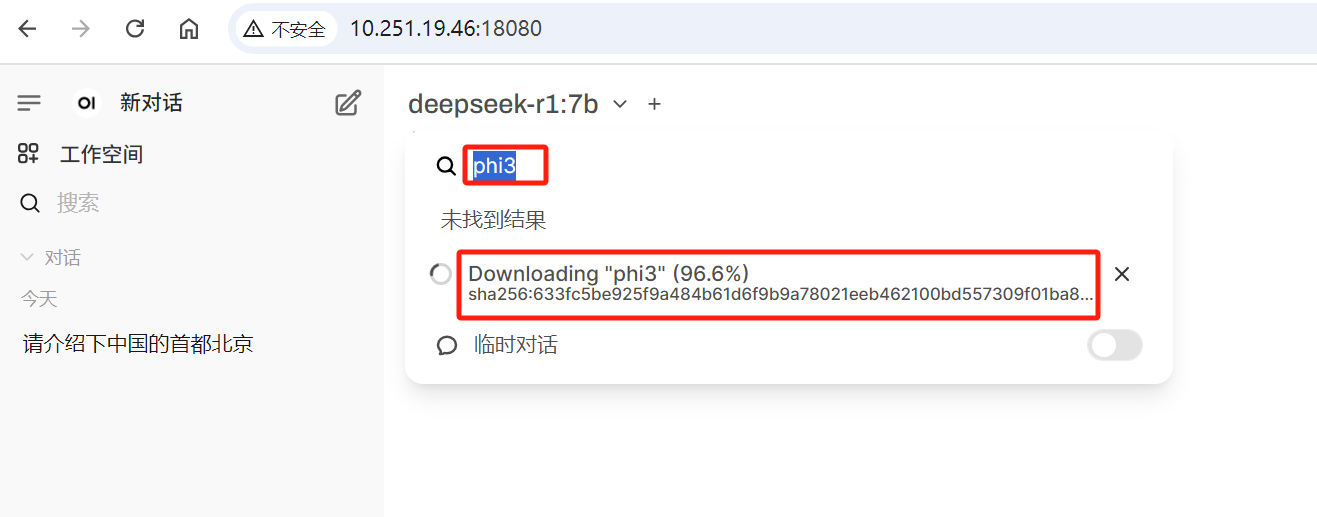
    • （5）在工作空间中基于基础LLM创建一个自定义LLM，如果基础LLM被隐藏了，则在会话的下拉模型列表中基础LLM不可见，自定义LLM可以被看见与使用；如果基础LLM被禁用了，则在会话的下拉模型列表中基础LLM不可见，此自定义LLM可以被看见但有一个“external”标识，使用时会报错提示“404: Model not found”

    • （6）以上关于隐藏的相关操作，对系统默认“管理员”角色中的用户都无影响。

1.2.4 数据库

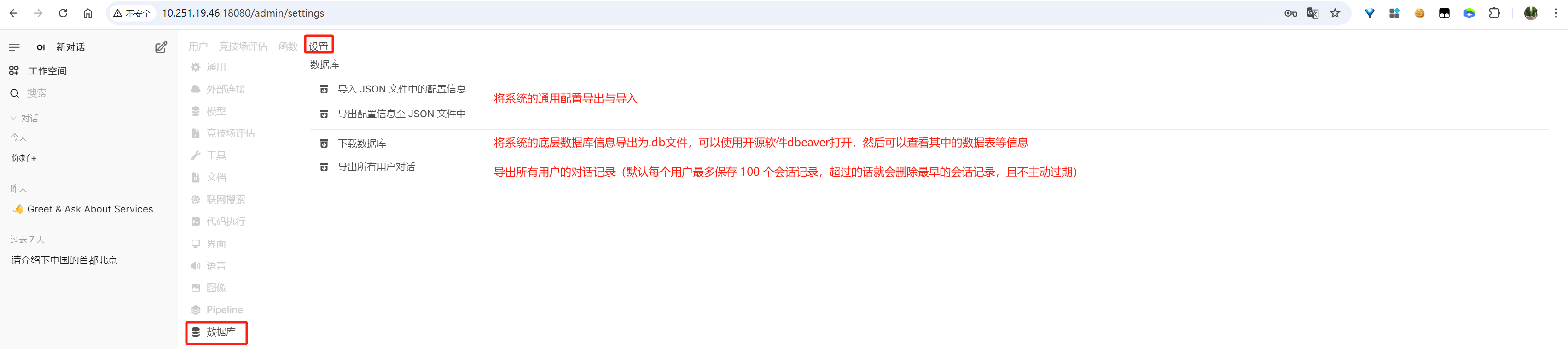
image-20250613141651657

将系统的通用配置导出与导入

将系统的底层数据库信息导出为.db文件，可以使用开源软件dbeaver打开，然后可以查看其中的数据表等信息

导出所有用户的对话记录（默认每个用户最多保存 100 个会话记录，超过的话就会删除最早的会话记录，且不主动过期）

image-20250611174745413 
1
2
(llamafactory) root@g406011748489384920:~# ollama list

二、工作空间

以“管理员”权限组的用户登录系统，才能看到与操作工作空间。

image-20250612125405289

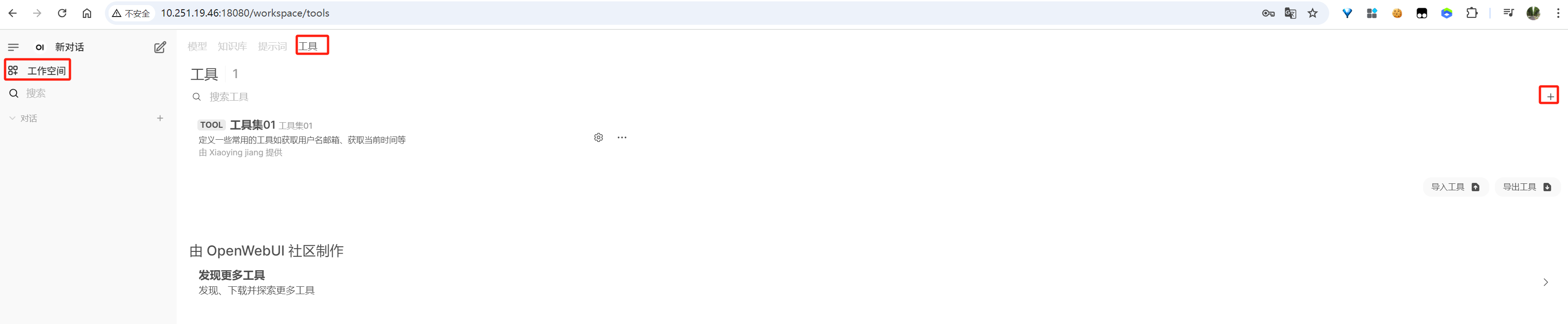
2.1 工具

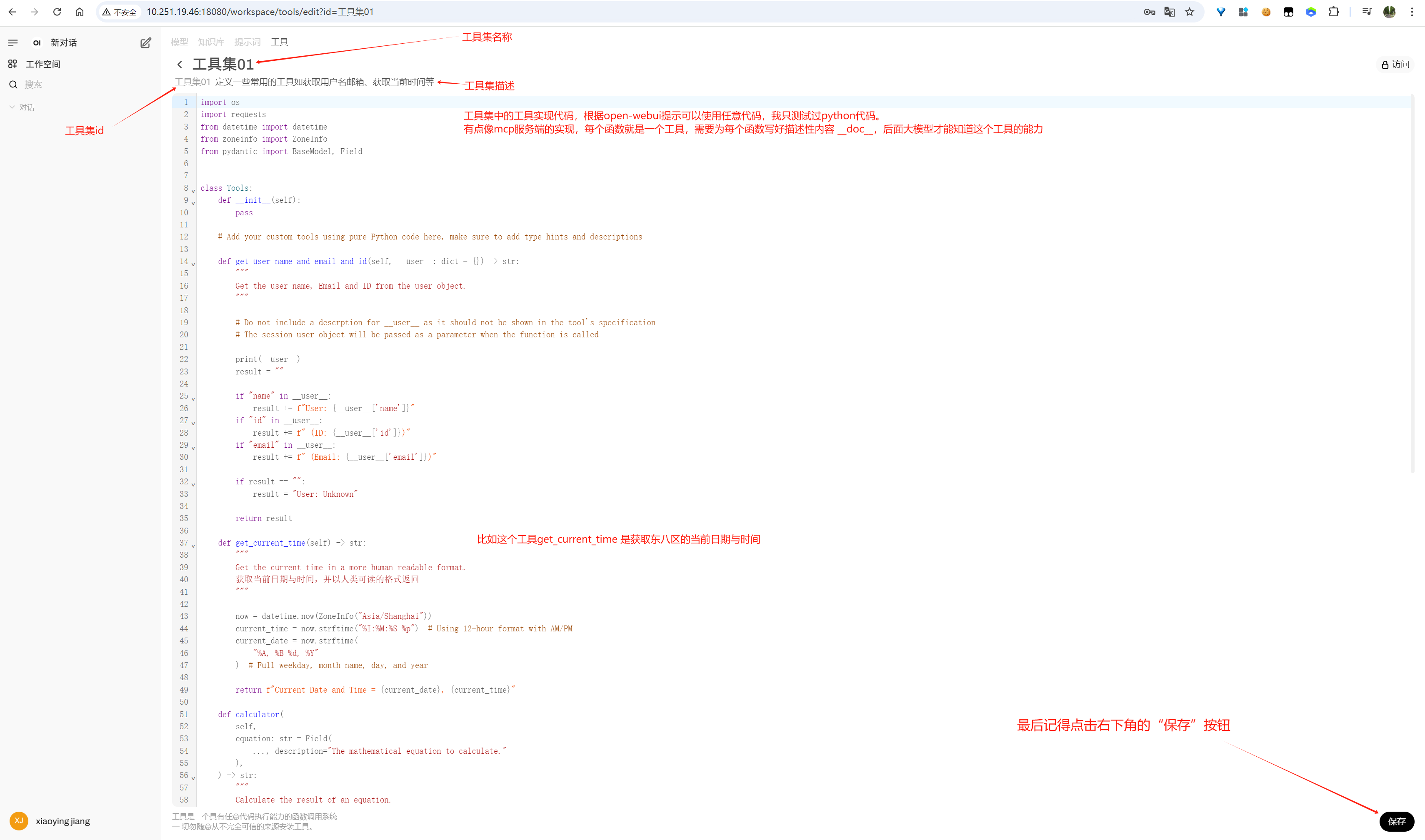
image-20250613150851408
image-20250613151519202

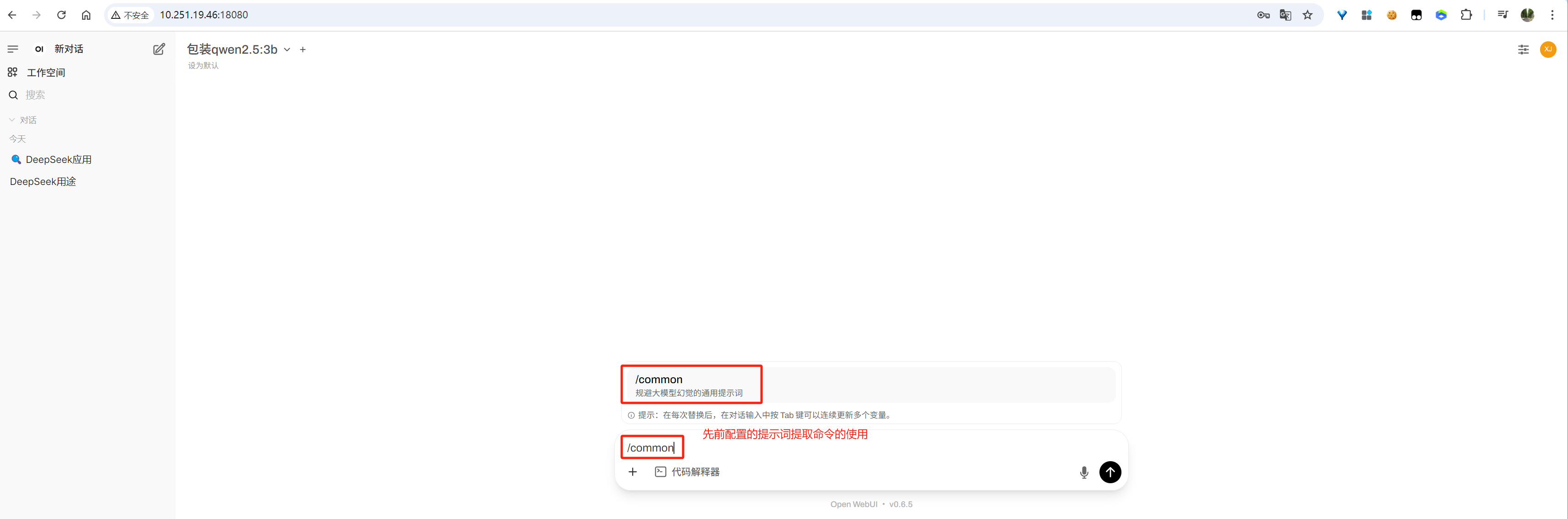
2.2 提示词

image-20250613153704366
image-20250613154010417 
1
2
3
4
5
\# 角色
## 你是一个聊天助手，能够提取用户提问中的关键词，并给出精简准确的回答。

# 强烈要求
## 如果你不知道提问的答案或者说没有掌握提问相关知识，请直接回复“对不起，我还没有掌握此提问相关知识”，不要凭空捏造内容进行回复。

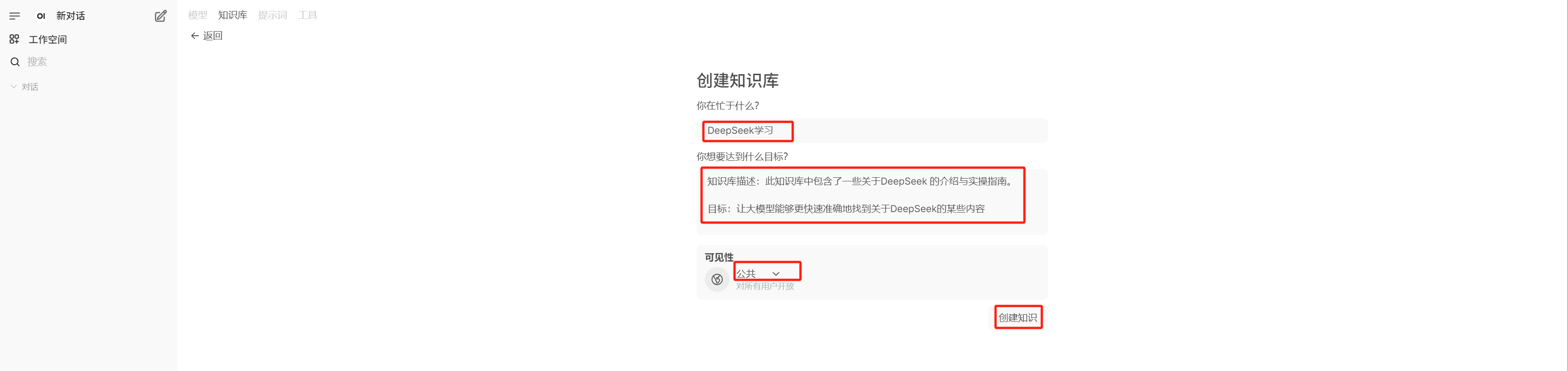
2.3 知识库

image-20250613154046905
image-20250613154222910
image-20250613154308566

上传文件到知识库中时，会使用嵌入模型将文件向量化，使用上述容器化方式部署open-webui 0.6.5时，默认使用的嵌入模型是sentence-transformers/all-MiniLM-L6-v2，可以通过如下命令查看：

1
2
3
4
5
6
7
8
9
#宿主机上
(llamafactory) root@g406011748489384920:~/.cache/modelscope/hub/models# docker inspect open-webui | grep EMBEDDING
                "USE_EMBEDDING_MODEL_DOCKER=sentence-transformers/all-MiniLM-L6-v2",
                "RAG_EMBEDDING_MODEL=sentence-transformers/all-MiniLM-L6-v2",

#容器化
root@e38be1309275:/app/backend# env | grep EMBEDDING
USE_EMBEDDING_MODEL_DOCKER=sentence-transformers/all-MiniLM-L6-v2
RAG_EMBEDDING_MODEL=sentence-transformers/all-MiniLM-L6-v2

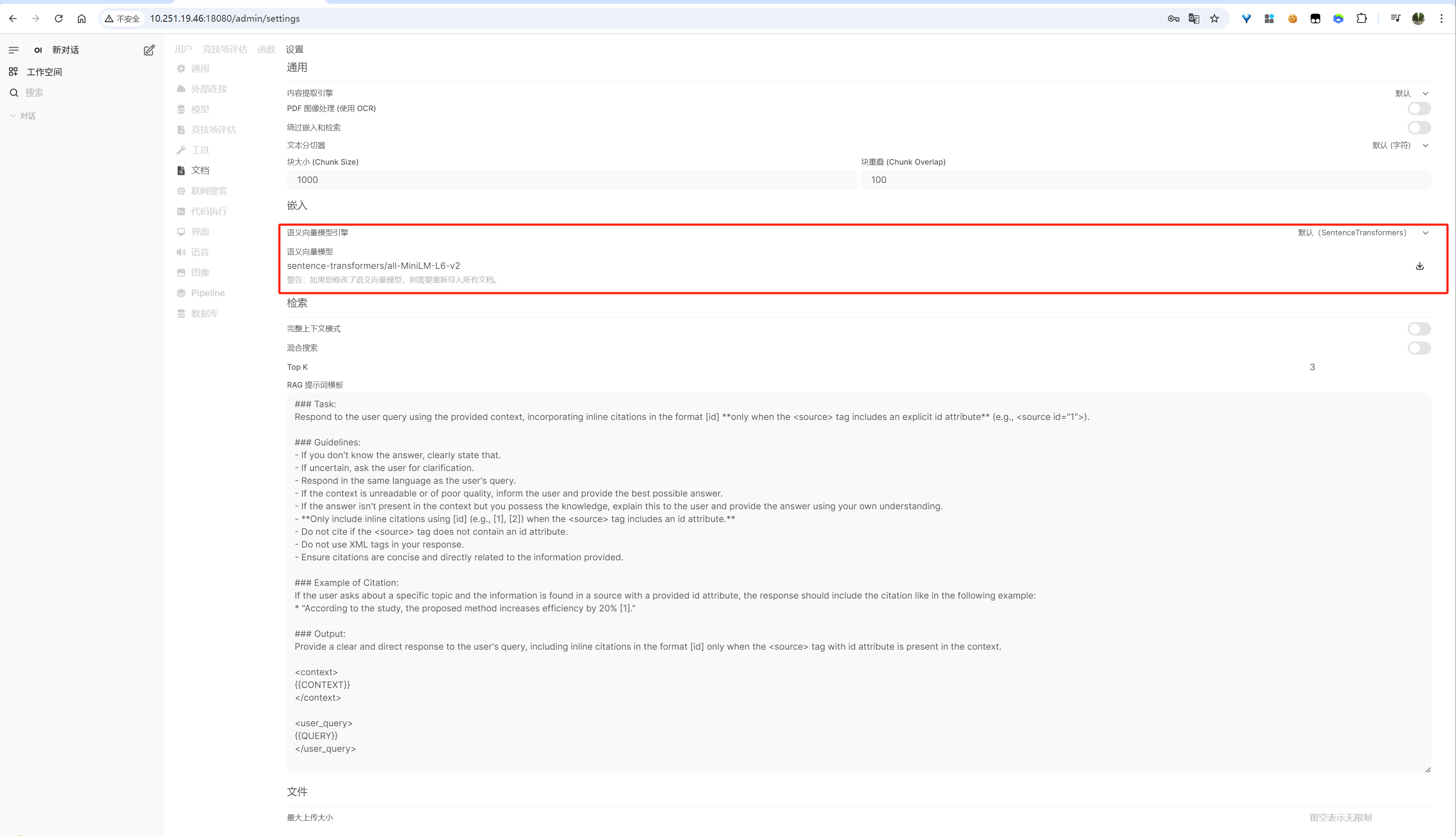
在管理员面板->设置->文档 页面，也可以看到嵌入模型及其相关向量化与召回配置：

image-20250613160635090

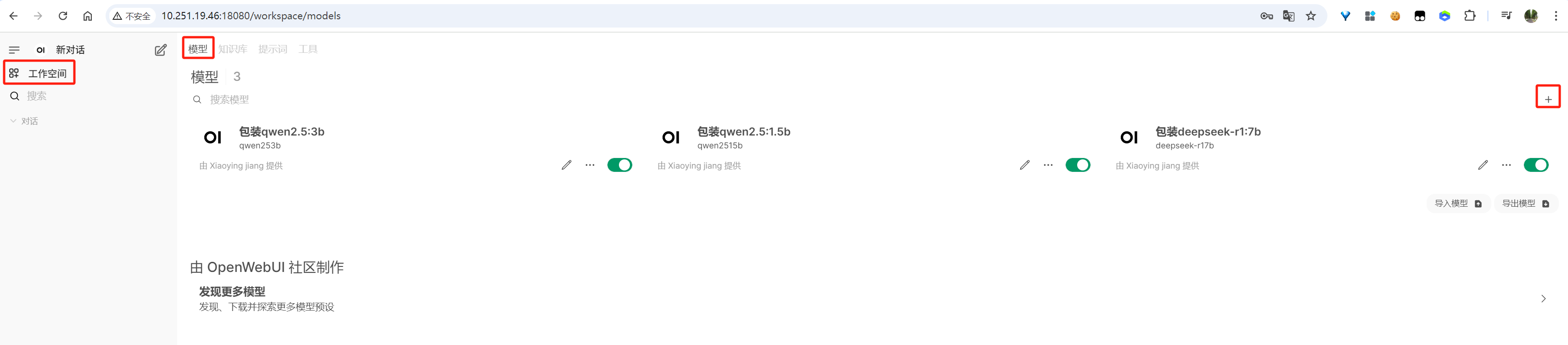
2.4 模型

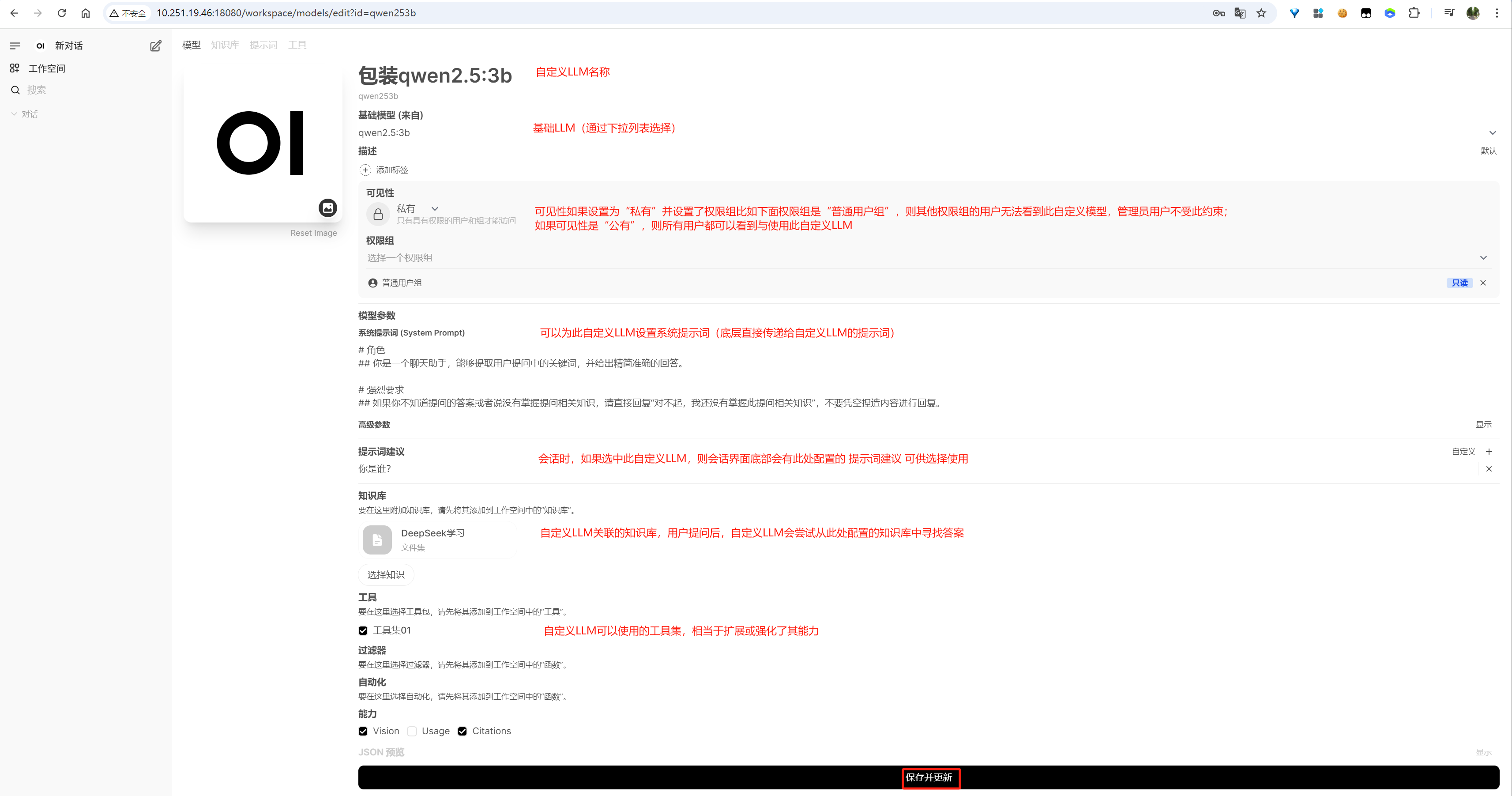
模型配置：

image-20250613160720802
image-20250613161637049

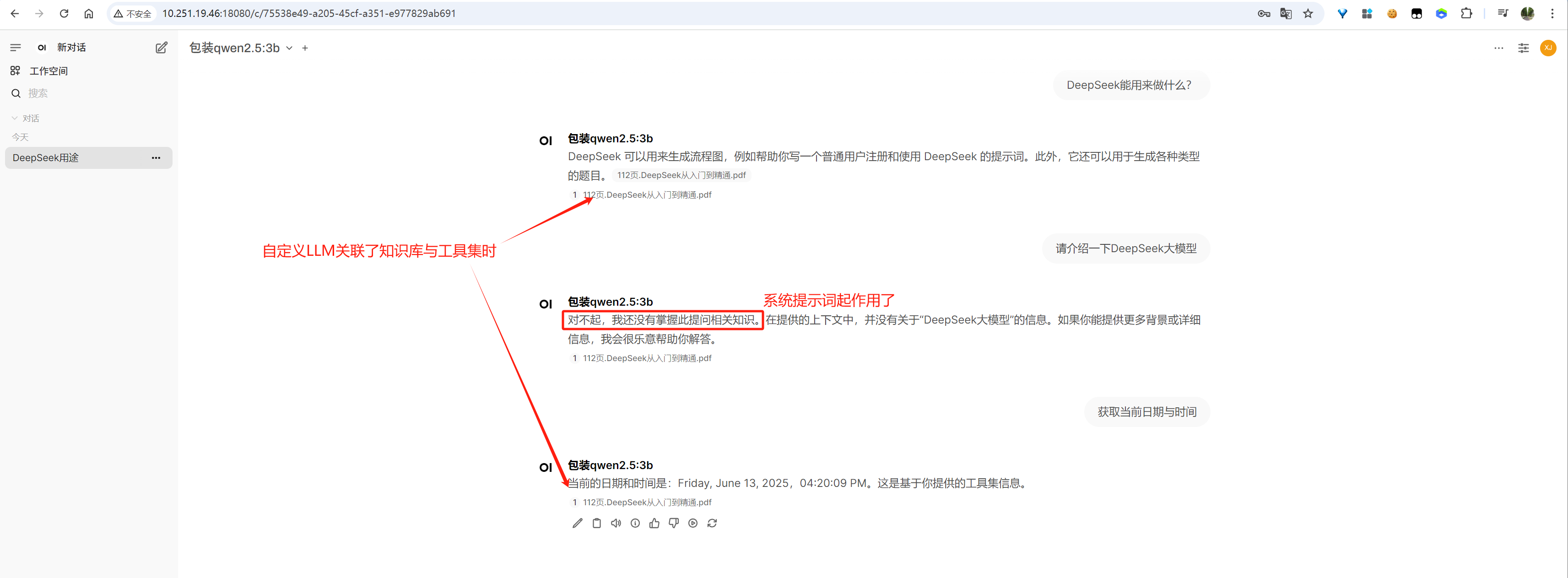
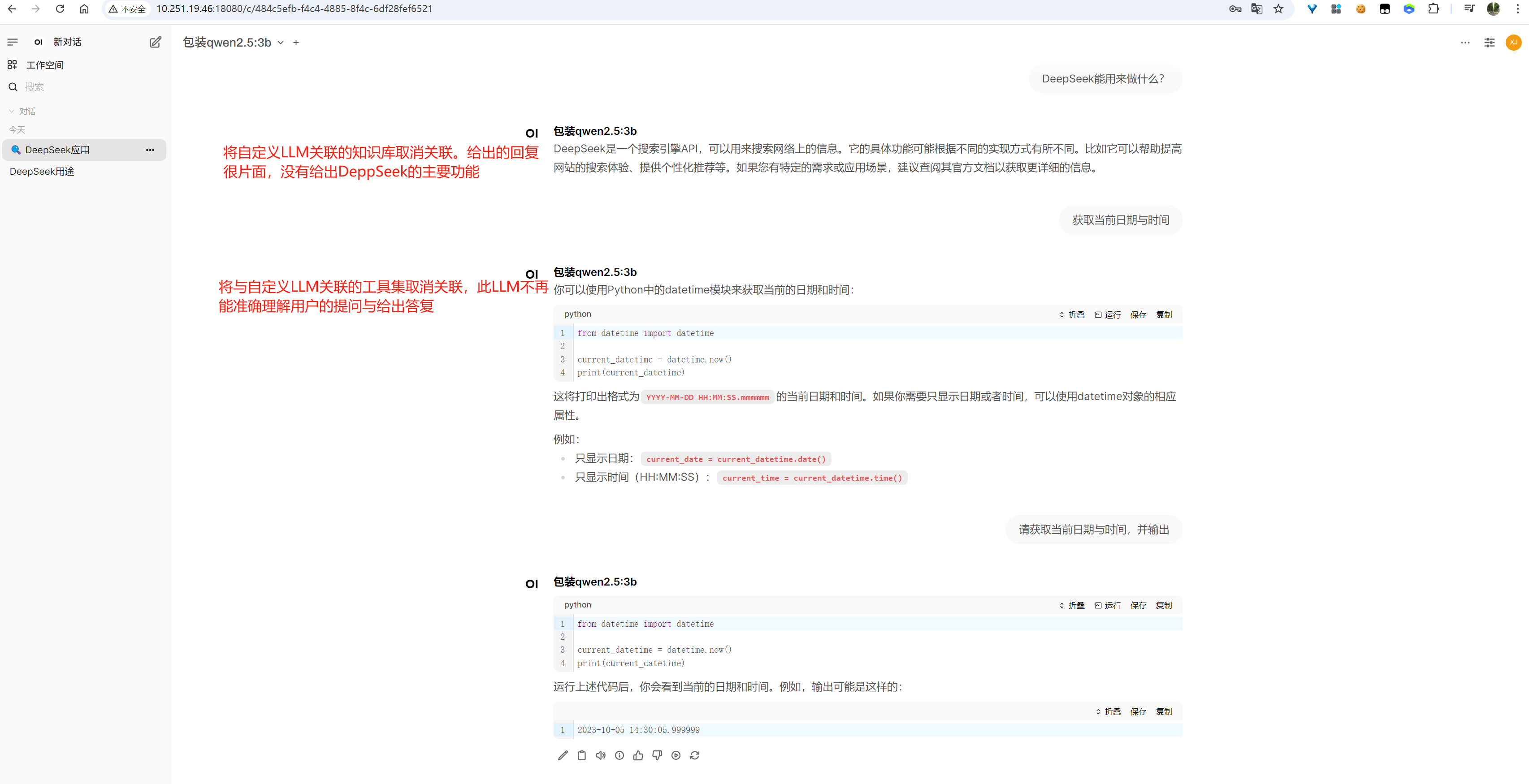
模型使用：

image-20250613162150701
image-20250613170340370
image-20250613170517086

三、设置

3.1 通用

image-20250613171150498

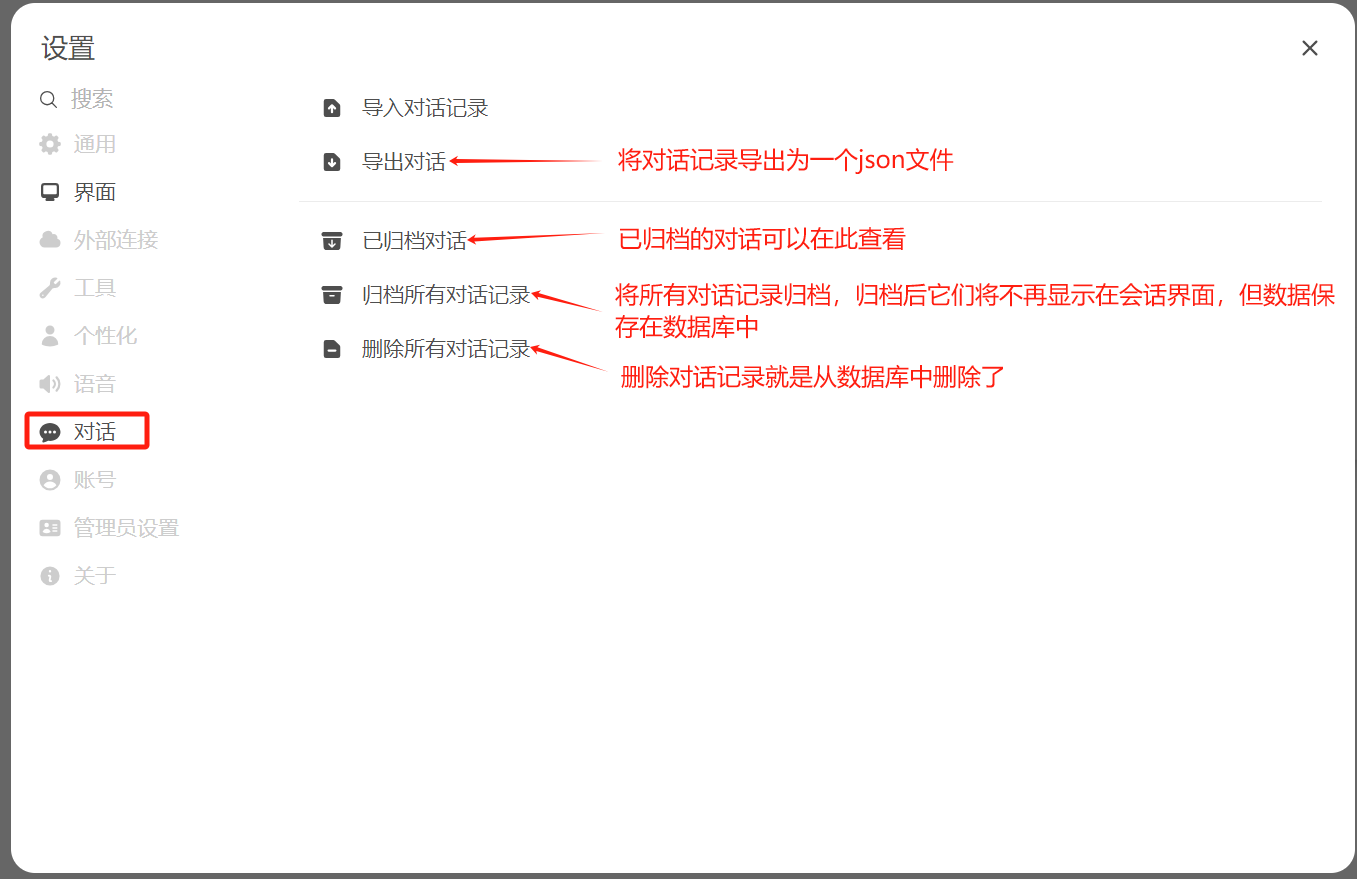
3.2 对话

image-20250613171931810

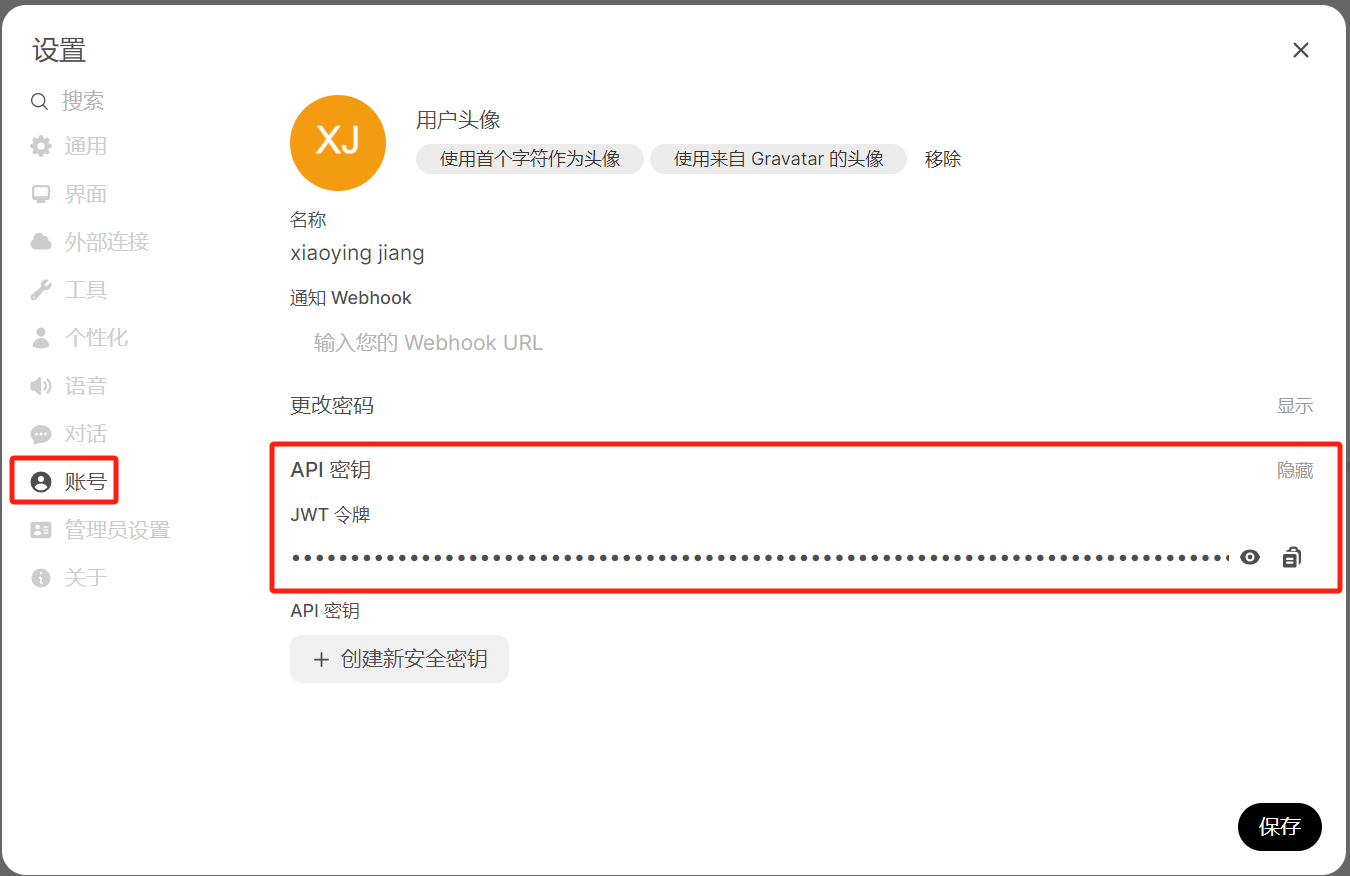
3.3 账号

image-20250613170815466

其实在 调用本地 Ollama 模型时，如果使用的是 OpenAI 兼容协议并通过 openai Python SDK 接入时，不会校验 api_key ，但必须有这个字段，所以可以随便填写一个值。

1
2
3
4
5
6
7
#查看所有LLM
(llamafactory) root@g406011748489384920:/opt/jiangsy# ollama list
NAME              ID              SIZE      MODIFIED     
qwen2.5:1.5b      65ec06548149    986 MB    25 hours ago    
phi3:latest       4f2222927938    2.2 GB    2 days ago      
qwen2.5:3b        357c53fb659c    1.9 GB    2 days ago      
deepseek-r1:7b    755ced02ce7b    4.7 GB    2 weeks ago
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#通过python sdk调用LLM示例
from openai import OpenAI

client = OpenAI(
    #api_key="sk-7800dc8fded44016b70814bf80f4c78f",
    api_key = "aaa",
    base_url="http://localhost:11434/v1"
)
models = client.models.list()

messages=[
        {"role": "system", "content": "You are a helpful assistant."},
        {"role": "user", "content": "证明必达格拉斯定理"}
    ]
params = {
        "model": "qwen2.5:1.5b",
        "messages": messages,
        "stream": True,
        "timeout": 600,
        "temperature": 0.0,
    }

stream = client.chat.completions.create(**params)

for chunk in stream:
    if not chunk.choices or chunk.choices[0].delta.content is None:
        continue

    print(chunk.choices[0].delta.content, end="")
print()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#调用成功，但LLM的回复是不正确的，此时需要对其进行微调或联网
(llamafactory) root@g406011748489384920:/opt/jiangsy# python call-llm-by-python-sdk02.py 
必达格拉斯定理（Perron-Frobenius Theorem）是线性代数和矩阵理论中的一个重要结果，它描述了非奇异的实对称矩阵的特征向量的一些性质。这个定理在许多领域都有应用，包括机器学习、信号处理和控制论等。

### 必达格拉斯定理的内容

必达格拉斯定理主要涉及的是一个实对称矩阵 \( A \) 的特征值和特征向量。对于非奇异的实对称矩阵 \( A \)，以下结论成立：

1. **最大特征值**：\( A \) 有一个最大的正实部特征值，称为 \( A \) 的 **谱半径**（spectral radius），记为 \( r(A) \)。
2. **特征向量的正性**：对于 \( A \) 的所有正实部特征值，对应的特征向量都是正向量。换句话说，如果 \( \lambda \) 是 \( A \) 的一个正实部特征值，则 \( x \) 是 \( A \) 对应的正向量。

### 证明

证明必达格拉斯定理通常涉及几个关键步骤：

1. **矩阵对称性**：首先，我们注意到 \( A \) 是一个实对称矩阵。这意味着 \( A = A^T \)，即 \( A \) 的转置等于它本身。
2. **特征值的性质**：由于 \( A \) 是实对称的，它的特征值是实数，并且可以被归一化为正实部的特征向量。

### 证明过程

1. **最大特征值的存在性**：
   - 首先，我们证明存在一个最大的正实部特征值。考虑 \( A \) 的所有特征值 \( \lambda_1, \lambda_2, \ldots, \lambda_n \)，其中 \( n = \text{rank}(A) \) 是矩阵的秩。
   - 由于 \( A \) 是实对称的，它的特征值是实数。因此，我们可以考虑这些特征值在复平面中的部分。

2. **正向量的存在性**：
   - 对于每个正实部的特征值 \( \lambda_i \)，我们可以通过归一化找到一个对应的正向量 \( x_i \)。
   - 由于 \( A \) 是非奇异的，它的秩等于其维度，即 \( n = \text{rank}(A) \)。这意味着存在一个正实部的特征值。

3. **最大特征值的存在性**：
   - 我们可以证明存在一个最大的正实部特征值。考虑所有正实部的特征值和它们对应的正向量。
   - 由于 \( A \) 是非奇异的，它的秩等于其维度，即 \( n = \text{rank}(A) \)。这意味着存在一个正实部的特征值。

### 结论

综上所述，必达格拉斯定理表明对于非奇异的实对称矩阵 \( A \)，它有一个最大的正实部特征值，并且对应于这个最大特征值的所有特征向量都是正向量。这在许多应用中是重要的，特别是在信号处理和控制理论中。

### 参考文献

- **参考文献**：《线性代数及其应用》（Linear Algebra and Its Applications），作者：Gilbert Strang
  - 这本书详细介绍了矩阵理论中的各种定理和证明方法。
AIGC
#AIGC
openwebui-v0.6.5学习02-常用配置与使用
https://jiangsanyin.github.io/2025/06/11/openwebui-v0.6.5学习02-常用配置与使用/
作者
sanyinjiang
发布于
2025年6月11日
许可协议