机器学习入门-03线性模型

第3章 线性模型

参考：《机械学习第1版第47次印刷-周志华著》、https://www.datawhale.cn/learn/content/2/65

西瓜书代码实战：https://github.com/datawhalechina/machine-learning-toy-code/blob/main/%E8%A5%BF%E7%93%9C%E4%B9%A6%E4%BB%A3%E7%A0%81%E5%AE%9E%E6%88%98.md

3.1 基本形式

以下内容如无特别说明，向量都是列向量。即w=(w₁;w₂;...;w_d)和x=(x₁;x₂;...;x_d)均为d行1列的列向量。

3.2 线性回归

给定数据集D={(x₁,y₁), (x₂,y₂), ... , (x_m,y_m)}，其中xi=(x_i1, x_i2, ..., x_id)，y_i∈R。

线性回归（linear regression）就是要觉得一个线性模型以尽可能准确地预测实值输出标记。

线性回归经常用到的一类算法就是最小二乘法，但最小二乘法不仅限于线性回归。

如果要将线性回归模型的的预测值逼近真实值y的衍生物，比如㏑^y ，此时即有㏑^y = ，此模型称为对数线性回归。

更一般地情况，对于连续可微函数g(·)，令y=g^-1(w^Tx+b)，此时得到的模型称为广义线性模型，其中函数g(·)称为联系函数。可以知道，对数线性回归模型就是广义线性模型在g(·)=㏑(·)时特例。

3.3 对数几率回归

对数几率函数： \[ y=\frac{1}{1+e^{-z}} \] 对数几率模型： \[ y=\frac{1}{1+e^{-(\mathbf{w}^T\mathbf{x}+b)}}\\ \] 对数几率： \[ y=\ln{\frac{y}{1-y}} \]

---

对率回归最大化“对数似然”，表达式变化的相关推导（其中相关说明在图片之前进行了说明）： \[ \begin{aligned} \mathbf{β}=(\mathbf{w};b) \\ \mathbf{\hat{x}}=(\mathbf{x};1) \\ \text{这样，就可以将}\mathbf{w}^T\mathbf{x}+b \text{改写成}\mathbf{β^T}\mathbf{\hat{x}} \\ \end{aligned} \]

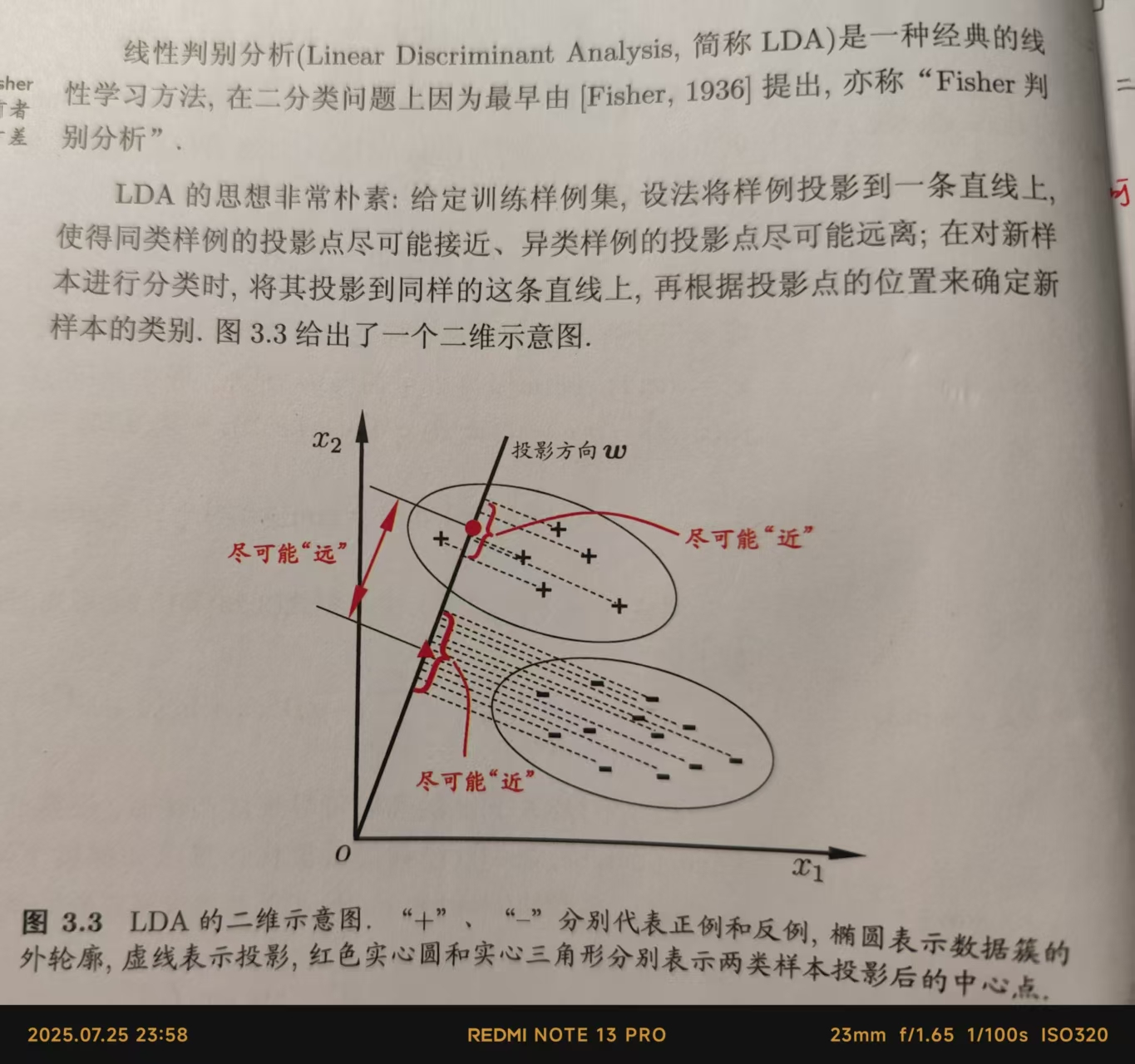
3.4 线性差别分析

均值向量

定义：均值向量（Mean Vector）提供了数据集中每个特征的平均值。对于 \[ \begin{flalign*} μ=[μ_1,μ_2,...,μ_m] \\ 其中μ_j=\frac{1}{n}\sum_{i = 1} ^m(x_{ij}) \\ μ_j是第j个特征的均值。 \\ x_{ij}是第i个观测的第j个特征值。\\ n是观测值的数量。 \end{flalign*} \] ​ 举例如下： \[ \begin{flalign*} 考虑身高和体重的数据集，包含4个观测值：\\ 身高: [160,165,170,175]\\ 体重: [55,60,65,70]\\ 平均身高: μ_{\text{身高}} = \frac{160 + 165 + 170 + 175}{4} = 167.5 \\ 平均体重: μ_{\text{体重}} = \frac{55 + 60 + 65 + 70}{4} = 62.5 \\ 因此，均值向量为: μ = [167.5, 62.5] \end{flalign*} \]

协方差矩阵：

定义：协方差矩阵（Covariance Matrix）描述了数据集中特征间的相互变化趋势。它不仅展示了单个特征的变异性（通过方差），还显示了特征之间的协方差。

对于m个特征，协方差矩阵是一个m×m矩阵，其中元素定义为: \[ \begin{flalign*} ∑_{jk}=\frac{1}{n-1}\sum_{i = 1} ^n(x_{ij}-μ_j)(x_{ik}-μ_k) \\ 其中：Σ_{jk}是特征j和特征k之间的协方差。\\ μ_j和μ_k分别是特征j和k的均值。\\ n是观测值的数量。\\ \end{flalign*} \] ​ 举例：使用上述身高和体重数据计算协方差矩阵。 \[ \begin{flalign*} \text{首先，我们已知:}\\ μ_{\text{身高}} = 167.5\\ μ_{\text{体重}} = 62.5\\ \\ \text{计算方差和协方差:}\\ \text{方差(身高): 使用公式计算得} \Sigma_{11} \\ \text{方差(体重): 使用公式计算得} \Sigma_{22} \\ \text{协方差(身高, 体重): 使用公式计算得} \Sigma_{12}、\Sigma_{21} \\ \\ \text{数据集：} \text{X=}\left[ \begin{matrix} 160 & 55 \\ 165 & 60 \\ 170 & 65 \\ 175 & 70 \end{matrix} \right] \\\\ \end{flalign*} \]

\[ \begin{flalign*} &(1)当j=1、k=1时,\Sigma_{11}=\frac{1}{4-1}[(160-167.5)^2+(165-167.5)^2+(170-167.5)^2+(175-167.5)^2]=\frac{125}{3}=41.67\\ &(2)当j=1、k=2时,\Sigma_{12}=\frac{1}{4-1}[(160-167.5)(160-62.5)+(165-167.5)(165-62.5)+(170-167.5)(170-62.5)+(175-167.5)(175-62.5)]=\frac{125}{3}=41.67\\ &(3)当j=2、k=1时,\Sigma_{21}=\frac{1}{4-1}[(55-62.5)(55-167.5)+(60-62.5)(60167.5)+(65-62.5)(65-167.5)+(70-62.5)(70-167.5)]=\frac{125}{3}=41.67\\ &(4)当j=2、k=2时,\Sigma_{22}=\frac{1}{4-1}[(55-62.5)^2+(60-62.5)^2+(65-62.5)^2+(70-62.5)^2]=\frac{125}{3}=41.67\\ \end{flalign*} \]

\[ \begin{flalign*} 经过上述计算，得到协方差矩阵如下：\\ C=\left[ \begin{matrix} 41.67 & 41.67 \\ 41.67 & 41.67 \end{matrix} \right]\\ \end{flalign*} \]

#也可以使用python代码实现均值向量与协方差矩阵的计算，如下：
import numpy as np

# 数据
heights = np.array([160, 165, 170, 175])
weights = np.array([55, 60, 65, 70])

# 计算均值
mean_height = np.mean(heights)
mean_weight = np.mean(weights)

# 计算方差和协方差
variance_height = np.var(heights, ddof=1)
variance_weight = np.var(weights, ddof=1)
covariance_height_weight = np.cov(heights, weights)[0, 1]

# 构造协方差矩阵
covariance_matrix = np.array([[variance_height, covariance_height_weight],
                              [covariance_height_weight, variance_weight]])

#打印到均值向量
print(f"均值向量: ({mean_height}, {mean_weight})\n")
#打印协方差矩阵
print(f"协方差矩阵: {covariance_matrix}\n")


###输出如下（可见使用python中相关科学计算库，可以极大地简化我们的计算工作）：
均值向量: (167.5, 62.5)
协方差矩阵: [[41.66666667 41.66666667]
 [41.66666667 41.66666667]]

3.5 多分类学习

一般情况下，我们可以利用二分类学习器来解决多分类问题。

一般地，如果有N个分类：C₁,C₂, ..., C_N，多分类 学习的基础思路是拆解法，即将多分类任务拆成若干个二分类任务进行求解。即训练时，对问题进行拆分，然后为拆分的每个二分类任务训练得到一个分类器；在测试时，这前面得到的多个分类器的预测结果进行综合与集成 ，获取最终的多分类结果。 此处的关键在于如何对多分类任务进行拆分、如何对多个分类器的结果进行集成。

常用的拆分策略有三种：一对一（One vs. One，简称OvO）、一对其余（One vs. Rest，简称OvR）、多对多（Many vs. Many，简称MvM）

3.6 类别不平衡问题

在类别不平衡时，常规的训练与测试方法已经失效或无意义，此时常采用《机械学习第1版第47次印刷-周志华著》2.3节中的查准率、查全率和F1来度量学习器的性能。