机器学习入门-04-决策树
第4章 决策树
4.1 基本流程
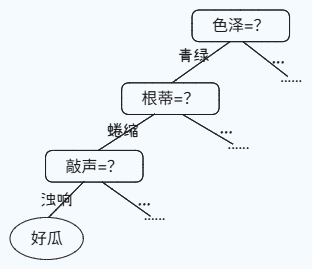
决策树是一种常见的机器学习方法。决策树又叫判定树,是基于树结构来进行决策的,是一种跟人类做决策很类似的、自然的处理机制。比如,我们如果要判别“某个瓜是好瓜吗?”这个问题时,我们通常会进行一系列的判断或子决策:它是什么颜色的?如果是青绿色的,我们再看它的根蒂是什么形态的?如果是蜷缩的,那我们看它敲起来是什么声音?如果是浊响的,那么我们可能能因此做出决策:“这是一个好瓜”。
决策树学习的目的是为了产生一棵泛化能力强即处理未见示例能力强的决策树,其基本流程遵循简单且直观的“分而治之”的策略。决策树学习基本算法如下:

4.2 划分选择
在决策树的算法过程中,有一个步骤需要选择最优划分属性(就是上图中的第8行)。总体来说,随着划分子结点的层数越大,我们总是希望决策树的分支结点所包含的样本尽可能属于同一个类别,即结点的纯度越来越高。
一般地,有如下4种方法来辅助我们选择最优划分属性:信息增益、增益率、基尼指数。
信息增益
著名的ID3决策树学习算法就是以信息增益为准则来选择划分属性的。
它的思想大致就是:从父结点到子结点,选择使得熵的减少量最大即信息增益最大的属性a来执行从父结点到子结点的决策。
公式细节待续。。。
增益率
著名的C4.5决策树学习算法就是以信息增益为准则来选择划分属性的。
它是在信息增益准则的基础发展而来或规避其不足而提出的,因为信息增益准则对可取值数目较多的属性有所偏好。但是增益率准则 对可取值数目 较少的属性又有所偏好,因为在实际场景中,C4.5并没有直接使用增益率最大的候选划分属性,而是使用了一个启发式思路:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
公式细节待续。。。
基尼指数
著名的CART决策树学习算法就是以信息增益为准则来选择划分属性的。
公式细节待续。。。
4.3 剪枝处理
剪枝是决策树学习算法对付“过拟合”的主要手段。
决策树剪枝的基本策略有预剪枝与后剪枝。预剪枝是指在决策树生成过程中,结每个结点在划分前进行估计,若当前结点的划分不能带来决策树泛化性能提升,则停止 划分并将当前结点标记为叶结点。后剪枝则是先从训练集生成一棵完整的决策树,然后自底向上地对非叶子结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为叶结点。
判断决策树逍化性能是否提升的方法,可以采用2.2节点中介绍的性能评估方法,如“留出法”,就是将数据集划分为训练集与验证集,在验证集上计算验证集精度看是否有所提升。
4.4 连续与缺失值
连续值处理
使用连续属性离散化技术,比如最简单的策略是采用二分法将连续属性进行处理。(C4.5决策树算法中就是使用此机制)