机器学习入门-05-神经网络
第5章 神经网络
5.1 神经元模型
各相关学科对“神经网络”的定义各不相同。以下是1988年T. Kohonen在Neural Networks创刊时对神经网络给出的定义。
神经网络定义:神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。
神经网络中最基本的元素或成分叫做 神经元模型,即上述定义中的所述的简单单元。 在生物神经网络中,每个神经元与其他神经元相连,当它“兴奋”时,就会向相连的其他神经元发送化学物质,从而改变这些神经元内的电位;如果某神经元的电位超过了一个“阀值”,那么它就会被激活,即“兴奋”起来,从而向其他相连神经元发送化学物质。
上述神经信号在神经元之间传递的过程可以被抽象如下简单模型:
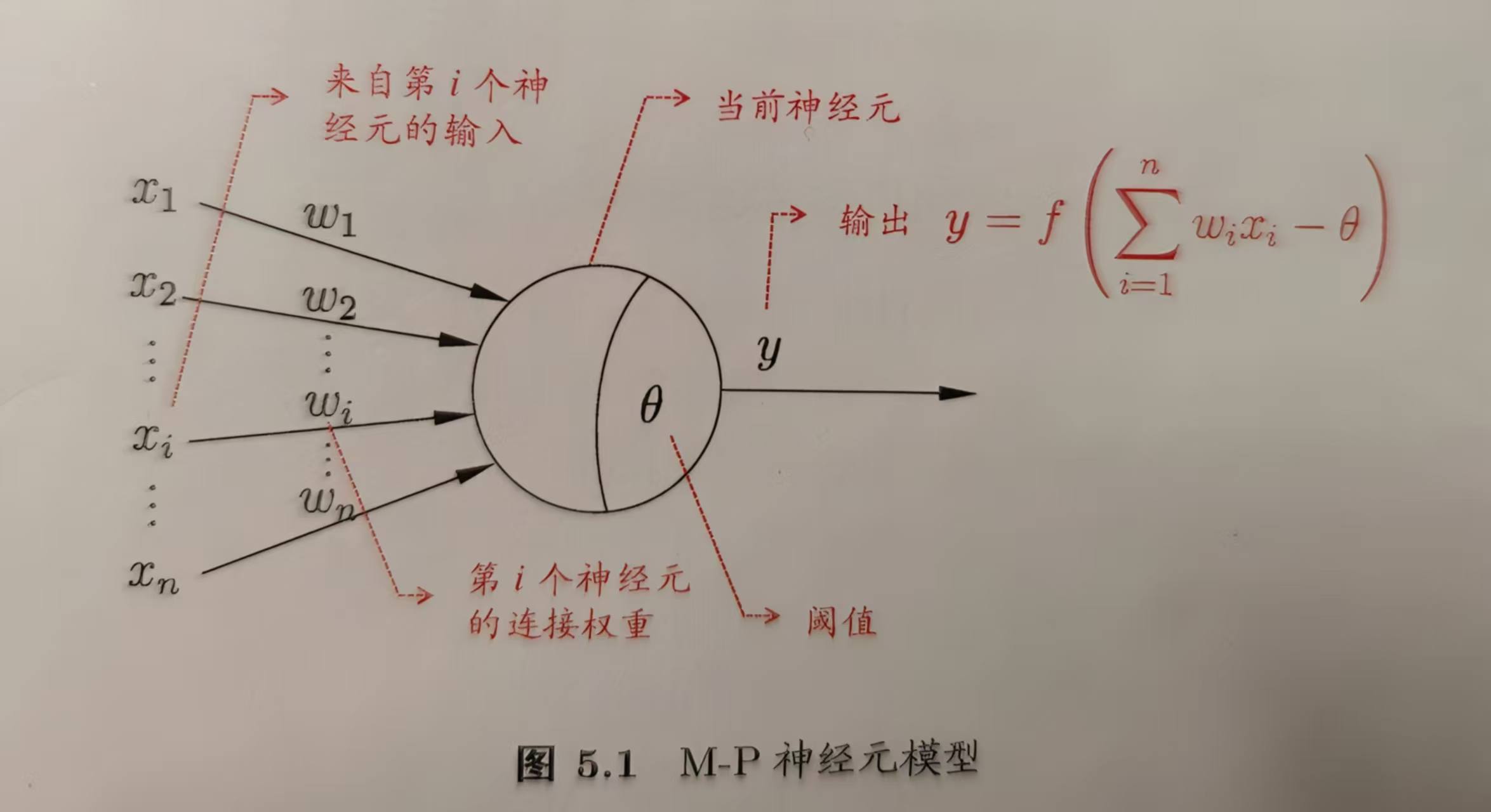
它于1943年由 McCulloch and Pitts提出,所以被称为M-P神经元模型,一直被没用至今。在上述这个模型中,神经元接收到n个其他神经元传递过来的输入信息,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值与神经元的阀值进行比较,然后通过“激活函数”处理以产生神经元的输出。理想的激活函数如果输出1,则表示神经元接收到的总输入值超过了神经元的阀值;如果输出0,则表示没有超过阀值。
理想的函数是如下图5.2(a)所示。因为其不连续、不光滑等不太友好的性质,我们会使用Sigmoid函数(其实就是我们前面章节看到的对数几率函数,它是Sigmoid函数的典型代表)替换阶跃函数sgn作为激活函数,Sigmoid函数有多个,典型的Sigmoid函数如下图5.2(b)所示。
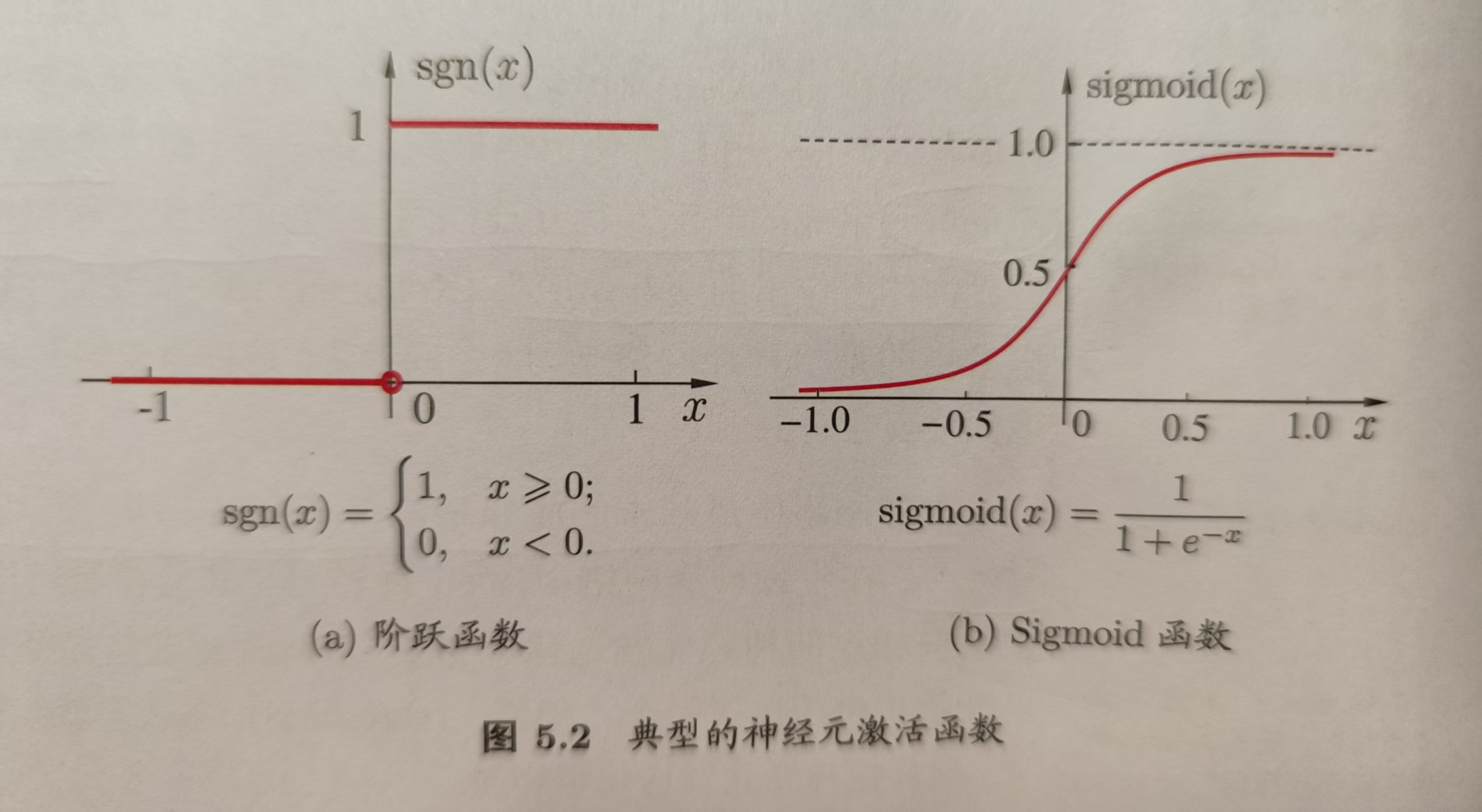
它将可能在较大范围内变化的输入值挤压到了(0,1)输出值范围内,所以有时也称为“挤压函数”。
5.2 感知机与多层网络
感知机由两层神经元组成。大致示意图如下图:
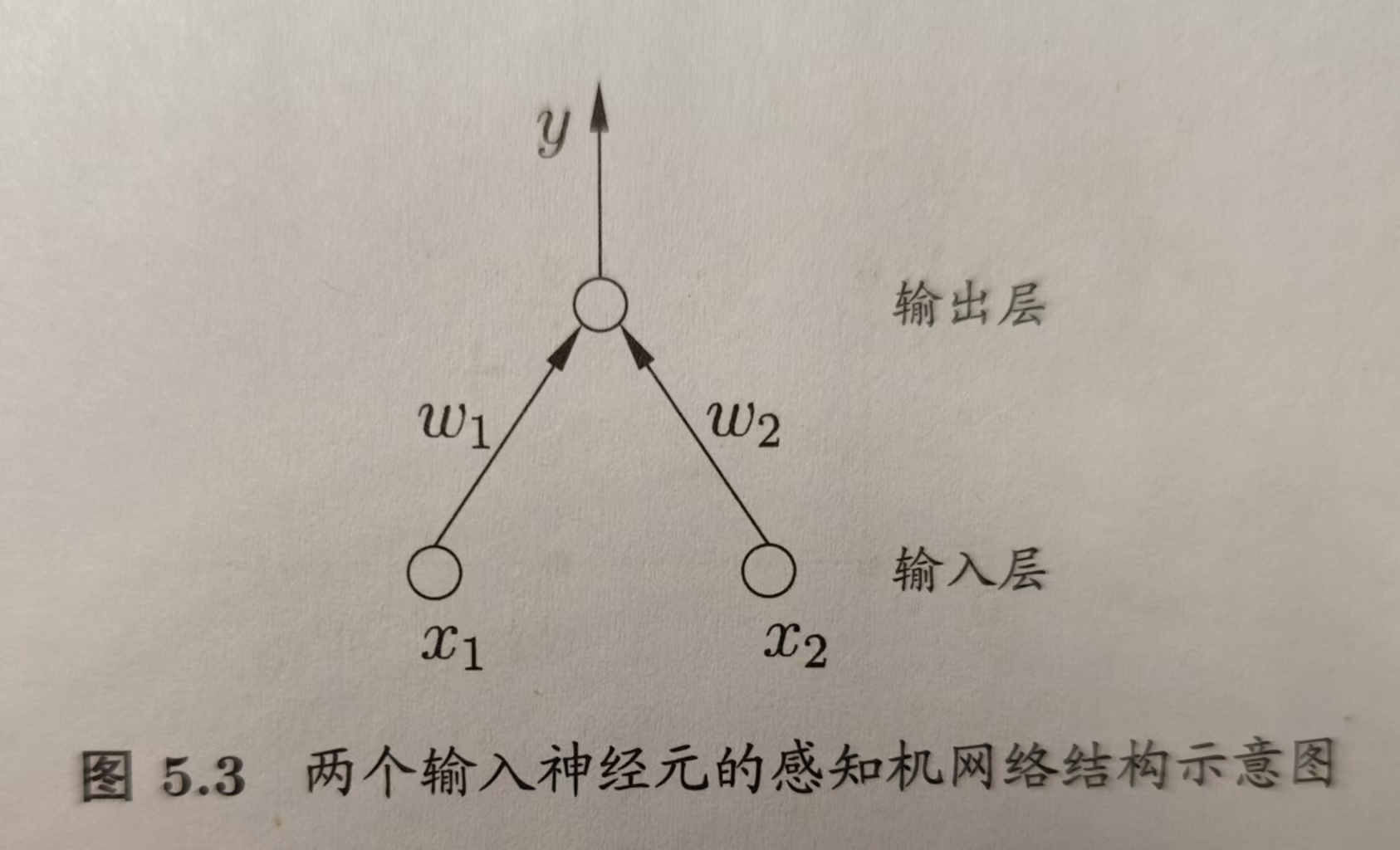
输入层接收输入信号后传递给输出层,输出层是M-P神经元,也被称为阀值逻辑单元。
感知机能够容易地实现逻辑与、或与非运算。令y=f( Σi(ωixi - θ) ),其中函数是阶跃函数。
- 令ω1=ω2=1,θ=2时,可以实现“x1与x2”
- 令ω1=ω2=1,θ=0.5时,可以实现“x1或x2”
- 令ω1=-0.6,ω2=0,θ=-0.5时,可以实现“非x1”;类似地也可实现"非x2"
对于两层神经元系统结构,给定训练数据集,权重ωi(i=1,2,...,n)以输出层神经元的阀值θ可以通过学习得到。如果将阀值θ看成一个固定输入为-1的哑结点的连接权重ωn+1,这样权重与阀值的学习就可以统一为权重的学习。此时其他n个输入层及其对应权重、加上此哑结点的输入即-1及其权重“θ”即为阶跃函数的总体参数值,阶跃函数计算此总体参数对应的函数值即可,结果即为输出层神经元的结果。
感知机的学习规则如下:对训练样本(x, y),若当前感知机的输出为ŷ,则感知机权重将可以如下这样调整: \[ \begin{aligned} & ω_i←ω_i+Δω_i, \quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,\,\,\,\,\,\,(5.1) \\ & Δω_i=η(y-\overset{\wedge}{y})x_i, \quad\quad\quad\quad\quad\quad\quad\quad\quad(5.2) \\ & 其中η∈(0,1),称为学习率。可知,如果感知机预测正确,则有y-\overset{\wedge}{y}=0 ,\\ & 此时Δω_i=0,则ω_i不再发生变化,否则会逐渐对ω_i进行权重调整 \end{aligned} \]
感知机只有一层功能神经元,即只有输出层神经元进行激活函数处理,所以其学习非常有限。
上述与、或与非问题都是线性可分的问题,可以证明,若两类模式是线性可分的,则存在一个线性超平面能将它们分开。
若要解决非线性可分问题,需要考虑使用多层神经功能神经元。常见的神经网络是形如下图所示的层级结构:每层神经元与下一层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接。这样的神经元结构通常被称为“多层前馈神经网络”。
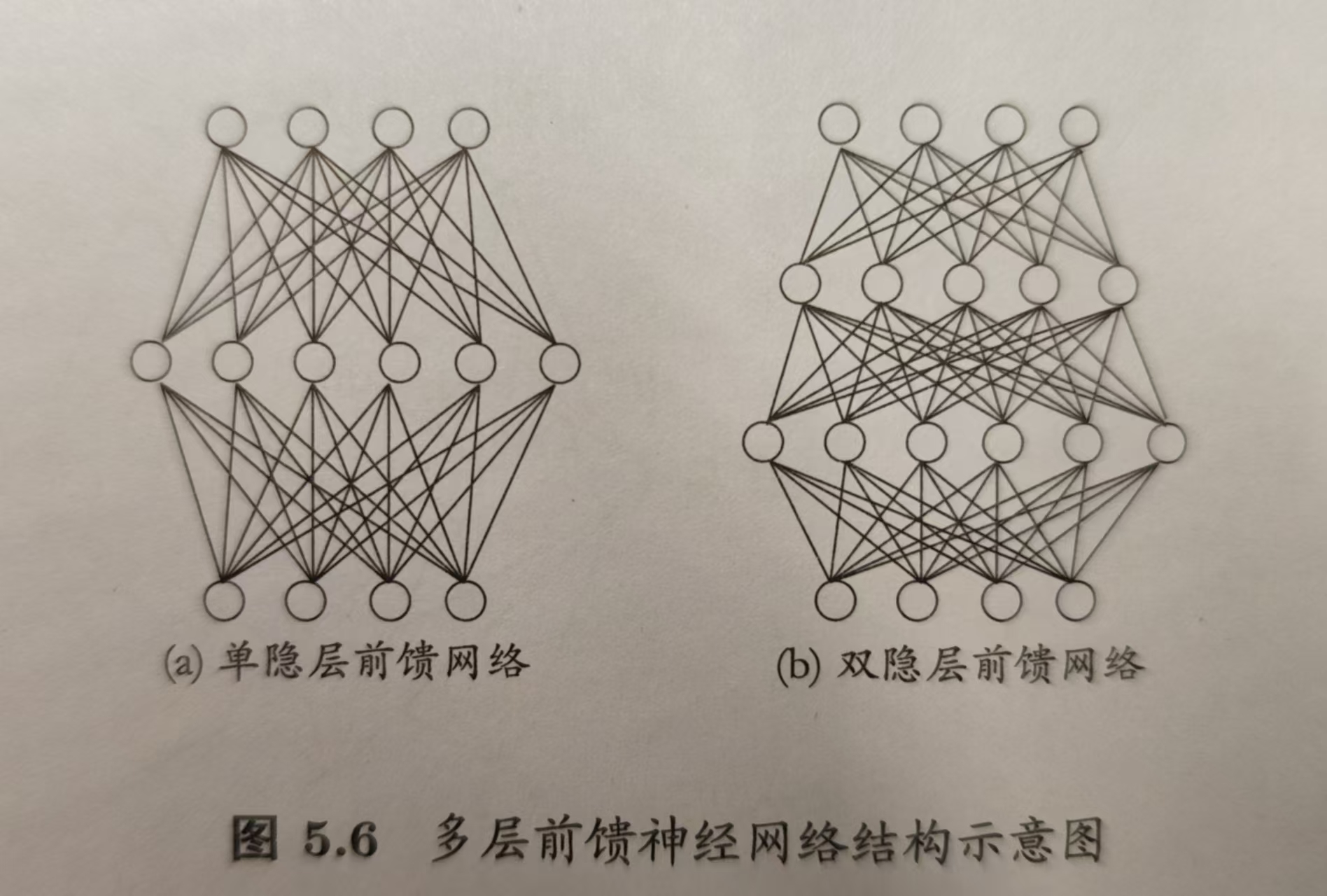
5.3 误差逆传播算法
误差逆传播(error BackPropagation,简称BP)算法是迄今为止最成功的神经网络学习算法 。此算法不仅适应于多层前馈神经网络,还可用于其他类似的神经网络如递归神经网络。
关于反向传播算法,自己暂时跟下面的步骤将公式大体上证明完成,但并未理解其中的意义!(记得自己以前单独证明过一次函数模拟二维直角坐标系中的点,是通过最小二乘法来计算误差的,在不断调整一次函数的k、b参数过程中,每轮调整两个参数后一次函数都是向误差的反方向进行偏移)


